12.1. ТЕПЛОВОЙ РАСЧЕТ ПРОЦЕССА ОХЛАЖДЕНИЯ

В задачу теплового расчета входит определение продолжительности охлаждения продуктов и количества теплоты, отводимого от них в процессе охлаждения.

Продолжительность охлаждения – основа расчета количества теплоты, отводимой от продуктов в процессе охлаждения, оценки эффективности работы холодильной камеры, оборудования и др. Она зависит от вида и параметров охлаждающей среды, размеров и теплофизических характеристик охлаждаемых продуктов. Наибольшей продолжительностью характеризуются процессы охлаждения продуктов в воздушной среде, наименьшей – в вакууме.

Продолжительность охлаждения продуктов, имеющих правильную геометрическую форму или близкую к ней, определяют, пользуясь номограммами, выражающими графическую зависимость безразмерной температуры от критериев Фурье и Био для середины пластины, оси цилиндра и центра шара.

Безразмерная температура

Θ = (t – t_o) / (t_H – t_j),     (50)

где t, t_H – соответственно текущая и начальная температуры продукта, °С;
t_o – температура охлаждающей среды, °С;

t = f (х, τ).     (51)

Критерий Био, характеризующий эффективность теплообмена поверхности продукта с охлаждающей средой, рассчитывается по уравнению

Bi = αl / λ,     (52)

где α – коэффициент теплоотдачи от наружной поверхности продукта охлаждающей среде, Вт/(м² • К);
l – половина толщины продукта, м;
λ – коэффициент теплопроводности продукта, Вт/(м • К).

Коэффициент теплопроводности продукта определяют по таблице (см. табл. 3), а коэффициент теплоотдачи – из критериальных зависимостей теплообмена при вынужденном и естественном движении охлаждающей среды у поверхности продукта.

Приближенно коэффициент теплоотдачи от продукта к воздуху находят из зависимости Юргенса:

α = 1,16 (5,3 + 3,6v),     (53)

где v – скорость движения воздуха у поверхности продукта, м/с.

Для приближенных расчетов коэффициент теплоотдачи от продукта к жидкой среде при естественной конвекции можно принять равным 200 – 230 Вт/(м² ·• К), при скорости движения жидкости 0,5 м/с - 1000 Вт/(м² ·• К).

По полученным значениям безразмерной температуры и критерия Bi из номограммы для пластины, цилиндра или шара (см. приложение 2) определяют точку пересечения соответствующих прямых. Из полученной точки опускают перпендикуляр на ось абсцисс и находят значение критерия Фурье Fo, или безразмерное время

Fo = аτ / l²,     (54)

где а – коэффициент температуропроводности продукта, м²/с;
τ – продолжительность охлаждения, с;
l – половина толщины продукта, м.

Отсюда продолжительность охлаждения

τ = Fo l²/a.     (55)

Коэффициент температуропроводности продукта а в формуле находят по таблицам теплофизических характеристик. В приближенных расчетах его можно принять равным 1,25 • 10^-7 м²/с.

Количество теплоты, отводимой при охлаждении, можно определить, пользуясь выражением

Q = G c_o (t_H – t_K)     (56)

Или

Q = G (i_H – i_K),     (57)

где G – масса продукта, кг;
с₀ – удельная теплоемкость продув та, кДж/(кг • К);
i_н – i_к – разность удельных энтальпий продукта при его начальной и конечной температурах, кДж/кг.

При охлаждении продуктов воздухом необходимо учитывать, что часть теплоты отводится вследствие испарения влаги с их поверхности, т.е. конвективный теплообмен сочетается с испарительным. Причем теплота, отводимая вследствие испарения влаги, может составлять до 50 % общего количества теплоты в зависимости от температуры воздуха и свойств охлаждаемых продуктов.

Испарение влаги с поверхности продуктов значительно уменьшается при наличии естественного защитного слоя или упаковки.

При медленном охлаждении продуктов количество теплоты, отводимой от мяса, птицы, рыбы и др., увеличивается за счет биохимических процессов, происходящих в продукте на начальной стадии созревания. В этом случае общая формула количества теплоты, отводимой от продукта, с учетом его внутренних тепловыделений и теплового эффекта испарения имеет следующий вид:

Q = G [c₀ (t_H – t_K) + q_BH + g(L_K – L_И)];     (58)

где G – масса продукта, кг;
t_H – t_K – разность начальной и конечной температур продукта;
q_ВН – внутреннее тепловыделение единицы массы продукта в процессе всего охлаждения, Дж/кг;
g – удельное количество испарившейся воды;
L_K – L_И – удельная теплота конденсации и испарения с единицы массы продукта, Дж/кг.

12.2. ТЕПЛОВОЙ РАСЧЕТ ПРОЦЕССА ЗАМОРАЖИВАНИЯ

При тепловых расчетах процесса замораживания задаются начальная и конечная температуры продуктов. Конечная температура замораживания практически никогда не бывает одинаковой во всех точках продукта. Однако при расчетах используют числовые значения теплофизических свойств продуктов, относящиеся ко всему процессу, которые берутся при средней их температуре за процесс.

Среднюю температуру продукта (в интервале от t₁ до t₂) при условии, что оба эти значения лежат в области от криоскопической температуры до температуры окончания льдообразования, можно определить по уравнению

t_ср = (t₂ – t₁)/ ln (t₂/t₁).     (59)

При замораживании температурное поле продукта остается равномерным до конца процесса, в связи с чем возникает необходимость введения понятия средней конечной температуры замораживания.

Средней конечной температурой замораживания называют температуру, характеризующую состояние замороженного продукта, помещенного в камеру хранения, когда наружный теплообмен практически отсутствует (температура на поверхности близка к температуре воздуха в камере), а внутренний происходит путем выравнивания температуры по всему объему продукта. Конечная температура продукта зависит от его размеров и теплофизических свойств, а также температуры теплоотводящей среды, коэффициента теплоотдачи. Она может быть рассчитана по формулам, полученным И.Г. Алямовским для тел различной геометрической формы:

для пластины     t_ск = (2_tц + t_n) / 2;     (60)

для цилиндра    t_ск = (t_ц + t_n) / 2;        (61)

для шара             t_ск = (2t_ц + 3t_n) / 2;    (62)

где t_ц и t_n – температура соответственно в центре и на поверхности продукта, °С.

Принимая во внимание то, что при замораживании большинства продуктов ниже -6°С (в центре) распределение температуры по их толщине становится близким к линейному, за среднюю конечную температуру замораживаемого продукта в приближенных расчетах можно принимать среднюю арифметическую между конечной температурой в центре и конечной температурой поверхности (31).

Для соблюдения постоянного температурного режима в камере хранения при внесении в нее продуктов сразу после замораживания необходимо, чтобы средняя конечная температура продукта после замораживания была равна температуре воздуха в камере хранения. Ее можно рассчитать по формуле

t_ц = 2 t_ск (Bi + 1) – t_o Bi / (Bi + 2);     (63)

Bi = α_м l / λ_м,      (64)

где α_м – коэффициент теплоотдачи при замораживании, Вт/(м² ·• К); К – коэффициент теплопроводности продукта при средней конечной температуре замораживания, Вт/(м • К).

В задачу теплового расчета процесса замораживания входит определение продолжительности замораживания и количества теплоты, отводимой при этом от продукта.

Продолжительность замораживания – время, необходимое для понижения температуры продукта от начальной до заданной конечной, за которое большая часть воды, содержащейся в тканях, превращается в лед. Оно зависит от теплофизических свойств продуктов, их толщины, формы, начальной и конечной температур замораживания, температуры и свойств охлаждающей среды.

Продолжительность замораживания продуктов τм можно определить, представляя их в виде тел простой стереометрической формы. В холодильной технологии для приближенных расчетов наиболее часто используют формулу Планка

τ_м = q_м γ_м lм (1/4 λ_м + 1/α_м) / [3,6 (t_кр – t_o) A],      (65)

где q_м – полная удельная теплота, отводимая от продукта при замораживании от начальной температуры до заданной средней конечной, кДж/кг;
γ_м – плотность замороженного продукта, кг/м;
l_м – толщина продукта, м; t_кp – начальная криоскопическая температура продукта, °С;
А – коэффициент, значение которого зависит от формы замораживаемого тела (для плоскопараллельной пластины А = 2, для бесконечного прямого круглого цилиндра А = 4, для шара А = 6);

q_м = i_н – i_ск,     (66)

где i_н – энтальпия продукта при начальной температуре, кДж/кг;
i_ск – энтальпия продукта при средней конечной температуре, кДж/кг.

Тело в форме цилиндра замерзает в два раза быстрее, чем тело в форме пластины, тело в форме шара – в три раза быстрее.

При расчете продолжительности замораживания упакованных продуктов формула Планка приобретает вид:

τ = q_м γ_м l_м {R / λ_м + P [1/α_м + ∑ (l_y / λ_y)]} / [3,6 (t_кр – t_o)],     (67)

где R и P – коэффициенты, значения которых зависят от соотношения размеров тела и направления тепловых потоков; ∑ (l_y / λ_y) – сумма тепловых сопротивлений слоев упаковки, м² • К/Вт.

При расчетах продолжительности замораживания по формулам Планка можно получить лишь приблизительные значения, так как не учитывается теплоемкость замороженной части тела, а также особенности строения и специфические свойства пищевых продуктов.

Количество теплоты, отводимой от продуктов при замораживании, можно определить по формуле

Q_м = G [c₀ (t_н – t_кр) + rωW + с_м (t_кр – t_ск)],     (68)

где G – масса замораживаемого продукта, кг;
r – скрытая теплота замерзания воды, Дж/кг;
ω – количество замороженной воды в продукте, определяемое при средней конечной температуре;
W – относительное содержание воды в продукте;
с_м – теплоемкость мороженого продукта, определяемая при средней температуре между криоскопической и средней конечной, Дж/(кг • К).

12.3. ТЕПЛО- И МАССООБМЕН ПРИ ХОЛОДИЛЬНОМ ХРАНЕНИИ

Хранение – неотъемлемая часть процесса консервирования пищевых продуктов и биологических материалов. С точки зрения теплофизических процессов хранение является стабилизацией режимных параметров на заданном уровне, обеспечивающем консервирование исходных свойств материала.

Цель хранения – увеличение срока годности продуктов питания путем замедления изменений, ухудшающих их качество, поэтому продолжительность хранения является одной из основных его характеристик. Продолжительность хранения τ зависит от физико- химических свойств материала, режимов холодильной обработки, хранения и других факторов, т.е.

τ = f (А, В, С, ..., N),     (69)

где А, В, С, ..., N – температура, влажность и скорость движения среды, ее состав и давление, наличие внешней оболочки (кожуры) и упаковки продукта и др.

Уровень значимости отдельных факторов различен. Температура, состав и скорость движения среды – основные регулируемые параметры процесса хранения. Их рассмотрим ниже. В настоящее время, как правило, продукты питания хранятся в воздушной среде. Изменение состава среды может улучшить условия хранения, т.е. удлинить его срок.

Как уже говорилось, существуют методы хранения в модифицированной газовой среде и в регулируемой среде. В первом случае материал хранится в упаковке, обладающей селективной способностью пропускать углекислый газ и выводить кислород. Недостаток такого метода – большая продолжительность создания определенного состава газовой среды, преимущество – максимальная защита продуктов от влияния внешних теплопритоков. Во втором случае материал хранится в регулируемой газовой среде, создаваемой в герметичных камерах при использовании газогенераторов, в которых происходит сжигание газа в присутствии катализатора. Такое хранение более совершенно. Рациональной можно считать среду, содержащую 2 – 3% СО₂.

Большое влияние на продолжительность хранения продуктов питания оказывает давление окружающей среды. Эксперименты показали, что хранение под давлением 0,15 МПа увеличивает срок хранения мясопродуктов в полтора раза. Таким образом, перспективным можно считать хранение в регулируемой среде при повышенных внешних давлениях. Естественно, внешняя оболочка (кожура) и упаковка продуктов питания уменьшают усушку и удлиняют продолжительность хранения, поэтому перспективно хранение охлажденных и замороженных продуктов в упакованном виде. Как уже отмечалось, продолжительность хранения зависит от Множества факторов, поэтому выявление аналитической зависимости от свойств материалов и режимов хранения – сложная задача. Кроме того, отсутствуют четкие критерии оценки результатов хранения. Однако основным параметром все же можно считать температуру хранения. Д. Г. Рютов на основе экспериментальных исследований предложил справедливую в пределах температур – 20 °С ≤ t ≤ -6 °С зависимость

τ = А · 10^-bt_в,           (70)

где А и b – постоянные, зависящие от свойств продуктов;
t_B – температура хранения, °С.

Приведем значение параметра А для некоторых продуктов: говядины и баранины – 2,15, свинины и нежирной рыбы – 1,78, кур – 1,58. Для всех этих продуктов b = 0,05. Для сливочного масла А = 2,85, b = 0,036.

В процессе хранения должна поддерживаться определенная температура. Ее повышение отрицательно сказывается на качестве хранящихся продуктов. За рубежом появились встроенные индикаторы, цвет которых изменяется при повышении температуры выше допустимой. Таким образом покупатель осведомлен о качестве купленного продукта. Работы по совершенствованию аналогичных датчиков продолжаются.

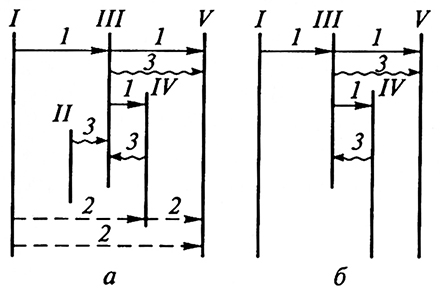
Рис. 19. Схема тепло- и массопереноса при холодильном хранении продуктов:
а – полная; б – упрощенная;
/ – наружные стены камеры; // – источники влаги помимо продукта;
/// – воздух камеры; IV – продукт; V – приборы охлаждения;
1 – перенос теплоту конвекцией; 2 – перенос теплоты радиацией;
3 – перенос теплоты испарением и конденсацией

На рис. 19, а дана принципиальная схема тепловлажностных процессов в камере холодильного хранения, предложенная Д. Г. Рютовым. В схеме учитываются конвективный и радиационный переносы теплоты, а также перенос влаги испарением (сублимацией) и конденсацией (десублимацией). Однако для математического описания процесса приняты некоторые допущения: влага в воздух камеры поступает только за счет испарения (сублимации) с поверхности продукта; продукт получает теплоту от воздуха только путем конвекции.

Упрощенная схема переноса теплоты и массы в камере холодильного хранения при отсутствии лучистого теплообмена и посторонних источников влаги дана на рис. 19, б. Температура продуктов t_n, хранящихся в камере, несколько ниже температуры хранения t_B из-за испарения воды с поверхности продукта (усушки).

Таким образом, в камере хранения поддерживается температура t_B > t_n > t_б, где t_б – температура охлаждающих приборов.

Условием переноса влаги будет

(t_в – t_п) < (t_в – t_б).     (71)

Количество теплоты, отбираемое от воздуха и расходуемое на испарение влаги в единицу времени, будет равно

Q = α F(t_B – t_п),     (72)

где α – коэффициент теплоотдачи между продуктом и воздухом, Вт/(м² ·• К);
F – площадь поверхности продуктов, м².

Количество влаги, испарившейся из продукта в единицу времени, кг/с,

W_и = βF (p_п – φp_в).     (73)

Она оседает на батареях охлаждения, причем

W_и = β_б F_б (φp_в – р_б).     (74)

где β, β_б – соответственно коэффициенты испарения и конденсации водяного пара, кг/(м² ·• с • Па);
F_б – площадь поверхности охлаждающих приборов, м²;
р_n, р_б – давление водяных паров соответственно на поверхности продукта, батареи, Па;
р_в – давление насыщенных паров воздуха, Па;
φ – относительная влажность воздуха.

Количество теплоты, затраченной на испарение, и количество испарившейся влаги связаны соотношением W_и = Q/r_n, где r_n – удельная теплота парообразования (сублимации), кДж/кг.

По закону Льюиса при испарении (сублимации) или конденсации (десублимации) α/β = const. Преобразовав уравнения (43) и (74), получим

αF/(α_бF_б) = А(φ р_в – p_б) / (t_B – t_n),     (75)

где α_б – коэффициент теплоотдачи между воздухом и поверхностью охлаждающей батареи;

А – постоянный коэффициент.

Анализ уравнения (75) показывает, что при данных F, α, t_B, t_п уменьшения усушки (φр_в – p_б) можно добиться, увеличивая α_бF_б, т. е. увеличивая поверхность охлаждающих приборов или коэффициент теплоотдачи α_б.

Математическое описание тепло- и массообменных процессов усложняется при учете лучистого теплообмена между продуктом, батареями охлаждения и стенками камеры, а также внутренних тепловых потоков, возникающих в результате колебания температуры воздуха в камере хранения.

Учитывая теплоту, подводимую к продукту конвекцией и излучением от более теплой стенки камеры, теплоту, отводимую от продукта излучением к поверхности приборов охлаждения, и теплоту сублимации влаги, а также внутренние тепловые потоки, усушку определяют из уравнения

ΔG = F_б (d_n – d_в) / [c_б (1/α_б + 1/ α_n)],     (76)

где F_б – площадь поверхности охлаждающих приборов, м²;
d_n, d_в – влагосодержание насыщенного воздуха соответственно при температуре продукта и воздуха камеры, кг/кг; с_б  – удельная теплоемкость влажного воздуха при температуре поверхности приборов охлаждения, кДж/(кг • К); α_n – конвективный коэффициент теплоотдачи от поверхности продукта, Вт/(м² ·• К).

Главный фактор, влияющий на усушку, – температура воздуха камеры хранения. Усушка уменьшается с понижением t_B, причем на каждые 10 °С приблизительно в два с половиной раза. Не случайно в настоящее время рациональной температурой хранения замороженных продуктов считается -25...-30 °С, при этом не только уменьшается усушка, но и удлиняется срок хранения продуктов. Однако в некоторых старых холодильниках еще используется температура -12 °С, а общепринятая температура равна -18...-20 °С.

Относительная влажность воздуха почти не влияет на усушку при низких температурах хранения. При одной и той же относительной влажности воздуха усушка может возрастать, когда возрастает разность температур между воздухом камеры и поверхностью приборов охлаждения, и убывать, когда уменьшается. Увеличение приводит к возрастанию интенсивности конденсации влаги из воздуха и, следовательно, к увеличению усушки. Скорость движения воздуха в камерах хранения должна быть минимальной, обеспечивающей ликвидацию застойных зон.

Абсолютная усушка практически не зависит от количества продукта в камере хранения, однако относительная усушка резко возрастает, когда камера недогружена. Это объясняется увеличением удельной плотности теплового потока на единицу продукта. Самый лучший способ сократить усушку до минимальной – упаковка продуктов и понижение температуры, причем потери массы зависят от паропроницаемости упаковочных материалов.

12.4. ТЕПЛО- И МАССООБМЕН ПРИ РАЗМОРАЖИВАНИИ

Процесс размораживания происходит при подводе теплоты к замораживаемому продукту. Количество теплоты, подводимой к размороженному продукту, находят по той же формуле, что и количество теплоты, отводимой при замораживании (68).

Различают два способа подвода теплоты к продукту. В первом случае теплота подводится путем теплообмена с внешней средой, причем внешней средой могут быть воздух, вода, пароводяная смесь или нагретые металлические плиты. В этом случае передача теплоты в продукте осуществляется теплопроводностью. Во втором случае теплота генерируется внутри продукта за счет поглощения энергии высокочастотных колебаний, которая переходит в тепловую.

Продолжительность размораживания при первом способе подвода теплоты сокращается с увеличением разности температур окружающей средой и поверхностью продукта; скорости циркуляции среды; относительной влажности воздуха; отношения F/V, где F – поверхность продукта, V – объем продукта.

Продолжительность размораживания при высокочастотном нагреве зависит от электрофизических характеристик продуктов и параметров установки. С увеличением частоты колебаний продолжительность размораживания уменьшается.

Процесс размораживания по первому способу условно делят на две стадии. Первая стадия – отепление материала до криоскопической температуры t_кp на его поверхности, осуществляемое конвективным теплообменом с окружающей средой. Вторая стадия – таяние льда, которое начинается на поверхности материала и заканчивается в области его термического центра. При этом основной механизм передачи теплоты в продукте – молекулярная теплопроводность как сухих веществ, так и влаги в виде воды или льда. При выводе формулы, определяющей продолжительность процесса, приняты следующие допущения: продукт представляет собой однородное изотропное тело в виде неограниченной пластины, температура окружающей среды и коэффициент теплоотдачи, теплоемкость, теплопроводность и плотность материала в процессе размораживания остаются постоянными.

Продолжительность первой стадии размораживания можно определить путем решения дифференциального уравнения теплопроводности dt/dτ = λ(d²t/dx²) при условии, что количество теплоты, подводимой к поверхности продукта, должно быть равно количеству теплоты, отводимой от поверхности внутрь продукта путем теплопроводности (граничное условие третьего рода):

α (t₀ - t_n) = -λ dt/dx.     (77)

 Коэффициент теплоотдачи α находят из известной критериальной зависимости

Nu = 0,032 Re^0,8.     (78)

Не приводя подробного решения дифференциального уравнения, представим продолжительность первой стадии размораживания в виде

τ = (l²/aμ₁²) ln[(t₀ – t_н) A₁ cosμ₁/(t₀ – t_кр)] ,        (79)

где а – коэффициент температуропроводности продукта, м²/с;
μ₁ – корень характеристического уравнения, находится в зависимости от Bi = αl/λ_np;
A₁ – коэффициент, определяемый корнем характеристического уравнения μ₁:

А₁ = (2 sin μ₁) / (μ₁ + sin μ₁ cos μ₁).     (80)

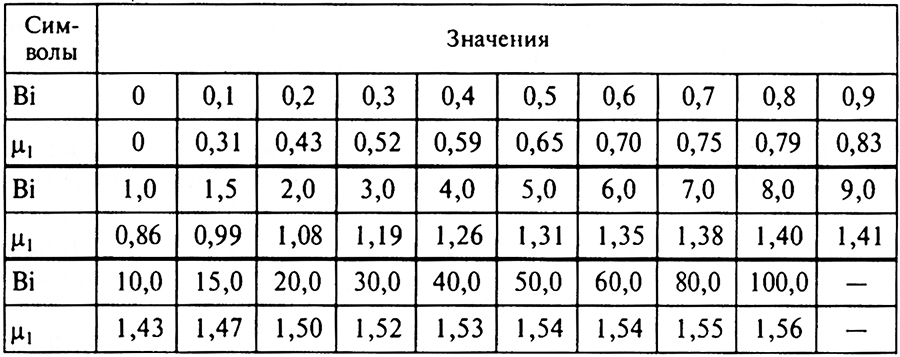
Так как корень характеристического уравнения μ₁ полностью определяется критерием Bi, то и постоянный коэффициент А₁ является однозначной функцией Bi. Существуют таблицы, по которым можно определить величину А₁, зная критерий Bi (табл. 4). Порядок расчета продолжительности первой стадии размораживания следующий:

1) определить коэффициент теплоотдачи α по критериальному уравнению (78) и критерию Re;

2) определить критерий Bi;

3) по табл. 4 найти μ₁ в зависимости от найденного критерия Bi;

4) определить постоянную А₁ по формуле (80) или из таблиц;

5) определить продолжительность первой фазы размораживания по формуле (79).

Эксперименты и расчеты показали, что длительность первой стадии размораживания составляет в среднем около 30 % длительности основной, второй стадии, поэтому в общую продолжительность процесса в дальнейшем будет введен коэффициент т = 1,3.

Таблица 4
Зависимость корня характеристического уравнения от Bi

При определении продолжительности размораживания на второй стадии процесса при появлении границы раздела фаз допускается, что распределение температур по толщине в размороженном слое имеет линейный характер, а температура границы раздела остается постоянной и равной криоскопической температуре tкр. Эти же допущения были приняты при выводе формулы продолжительности замораживания материала. Так как физическая модель этих процессов одинакова и одинаковы сделанные допущения, можно воспользоваться формулой Планка:

τ = [qγl / (t₀ – t_кр) K_ф] [(l / (2λ₀)) + (1/α)],     (81)

где q – удельное количество теплоты, которое необходимо подвести к продукту при размораживании;
γ – плотность продукта;
l – половина определяющего геометрического размера продукта;
К_ф – коэффициент формы продукта;
λ₀ – коэффициент теплопроводности размороженного слоя.

Полная продолжительность размораживания

τ = [qγl / (t₀ – t_кр) K_ф] [(l / 2λ₀) + (1/α)] m,     (82)

где т – коэффициент, учитывающий первую стадию размораживания.