Неструктурированные модели описывают только количество биологической фазы. Такие модели не учитывают и никоим образом не отражают состав биофазы, т. е. то, что можно назвать ее качественными характеристиками. Если в процессе роста существенно изменяется состав клеточной популяции и если это изменение влияет на кинетику клеточного роста, то анализ таких систем возможен только с помощью структурированных моделей. Поскольку ни в одной модели практически невозможно учесть материальные балансы всех компонентов клетки, то при создании структурированной модели (по необходимости приближенной) мы, очевидно, должны тщательно отобрать ключевые переменные и процессы, играющие важнейшую роль в планируемом применении этой модели. Как мы покажем на ряде примеров в следующих разделах, структурированные модели могут быть построены на основе различных концепций.

В структурированных моделях в качестве переменных биофазы обычно применяются массовая (x_i) или молярная (с_i) концентрации в единице объема биофазы [15]. При условии полного перемешивания уравнение материального баланса по компоненту j можно записать в следующем виде:

где ρ_с – плотность клеток, равная массе клеток в единице объема клеток; r_fi –молярная скорость образования компонента j [(число молей j) • (время)^–1·• (единица объема клеток)^–1]; Φ_x – масса клеток, вводимых в реактор в единицу времени; V_r – объем культуры; x– концентрация клеточной массы [(масса клеток) • (единица объема культуры)^–1]; с_i  – (число молей j) • (единица объема клеток)^–1. В последнем слагаемом уравнения (7.65) принимается, что вводимые в реактор (например, в рецикле) или выводимые из реактора клетки находятся в том же состоянии, что и популяция клеток в реакторе. Если это условие не выполняется (например, во втором или одном из последующих реакторов в каскаде ПРПП), то уравнение баланса должно быть соответствующим образом модифицировано.

Если допустить, что плотность клеток рс и объем культуры не изменяются во времени, то после дифференцирования уравнения (7.65) получим
            (7.66)

Для реактора периодического действия Ф_x равно нулю, а выражение в скобках в правой части уравнения (7.66) есть не что иное, как удельная скорость роста μ; следовательно, для этого случая уравнение (7.66) преобразуется следующим образом:
      (7.67)

Физический смысл r_fi ясен; выражение– µC_i отражает снижение концентрации, обусловленное разведением в процессе роста популяции клеток. Интересно, что оценка правой части уравнения (7.66) для ПРПП при стерильности питательных веществ опять-таки приводит к уравнению (7.67).

7.4.1. Компартментальные модели

В простейших структурированных моделях предусматривается компартментация биомассы в небольшом числе компонентов. Иногда эти компоненты имеют приближенное биохимическое толкование, например синтетический компонент (РНК и предшественники) и структурный компонент (ДНК и белки). Компартменты могут быть также определены как ассимилирующий компонент и синтетический компонент. В другой интерпретации при создании простых компартментальных моделей используется понятие об узких местах метаболизма.

Использование структурированных моделей с небольшим числом переменных оправданно также с точки зрения некоторых принципов динамики систем. Каждый тип реакций и транспортных явлений, осуществляющихся в популяции клеток (молекулярные соударения, химические реакции, диффузия, кругооборот РНК, синтез белков, увеличение числа клеток, завершение периодического процесса, спонтанные мутации), характеризуется своим временем релаксации, т. е. временем, необходимым для перехода в стационарное состояние после возмущения (вспомните разд. 3.1). Время релаксации может изменяться от долей секунды до нескольких часов. С точки зрения динамики систем в моделировании наиболее важна взаимосвязь между диапазоном времени, в течение которого совершаются изменения в среде (τ_E), и спектром времен релаксации внутриклеточных процессов. Можно допустить, что клеточные процессы, характеризующиеся быстрой реакцией на изменения в среде (т.е. небольшой величиной отношения времени релаксации к τ_E), находятся в квазистационарном состоянии (разд. 3.2.1). В другом крайнем случае, когда время релаксации некоторых клеточных процессов велико по сравнению с τ_E, эти клеточные процессы можно считать «замороженными» в начальном состоянии. Примером могут служить глубокие генетические изменения, которые практически никогда не осуществляются в ходе одного периодического процесса.

Установлено, что в случае многих сложных систем только два или три временц релаксации находятся в том же временном диапазоне, что и изменения в среде; этот факт еще раз: подтверждает обоснованность приближенного описания динамики сложных систем с помощью упрощенной модели с двумя или тремя переменными. В то же время часто трудно или даже невозможно связать некоторые из этих переменных с измеряемыми физическими количественными характеристиками системы. Ниже мы рассмотрим некоторые примеры простых компартментальных кинетических моделей роста клеточной популяции.

Уильяме предложил двукомпартментальную модель, которая удивительно точно описывает некоторые стороны динамики клеточного роста в периодическом процессе [16]. Основные постулаты этой модели формулируются следующим образом:

1. Синтетический компонент (1) продуцируется в результате поглощения внешнего питательного вещества S с экономическим коэффициентом Y (отношение массы компонента 1 к массе субстрата). Реакция образования синтетического клеточного компонента имеет первый порядок по общей плотности клеток x (отношению клеточной массы к объему культуры) и по массовой концентрации питательного вещества (отношению массы субстрата к объему культуры).

2. Структурно-генетический компонент клетки (2) продуцируется из компонента 1 со скоростью, пропорциональной ρ₁ρ₂ (ρ_i – отношение массы i к единице объема клеток).

3. Для деления клетки необходимо и достаточно удвоение компонента 2. Следовательно, численная плотность клеток пропорциональна концентрации компонента 2 в культуре.

4. Биомасса построена только из компонентов 1 и 2.

Для реактора периодического действия при условии полного (перемешивания эти же постулаты можно выразить в математической форме: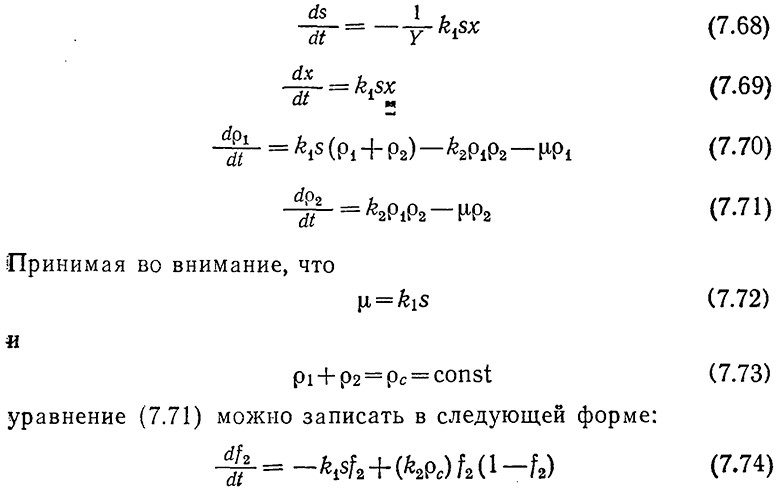
   
где f₂ = ρ₂/ρ_с представляет собой долю клеточной массы, состоящей из компонента 2. С помощью двух уравнений этой модели s можно выразить через х. Если таким путем преобразовать уравнение (7.69), то мы получим выражение, по форме совпадающее с уравнением (7.51). Следовательно, изменение x будет подчиняться логистическому уравнению типа (7.52).

Предложенный Уильямсом подход применялся для моделирования роста популяции клеток в периодическом процессе с использованием инокулята, находящегося в стационарной фазе в среде с истощенным питательным веществом, что соответствует ρ₁ = 0. Полученные таким путем результаты приведены на рис. 7.22; они хорошо воспроизводят некоторые часто наблюдаемые на практике особенности роста культур микроорганизмов в периодическом процессе, включая:

1. Лaг-фазу, в течение которой возрастают размеры клеток.
2. Фазу экспоненциального роста, в которой размер клеток достигает максимума.
3. Изменения в составе клеток в цикле роста. Поскольку такие изменения, очевидно, происходят даже в экспоненциальной фазе, отсюда следует, что рост клеток идеально не сбалансирован ни в одной из фаз роста.
4. Стационарную фазу с относительно небольшими клетками.

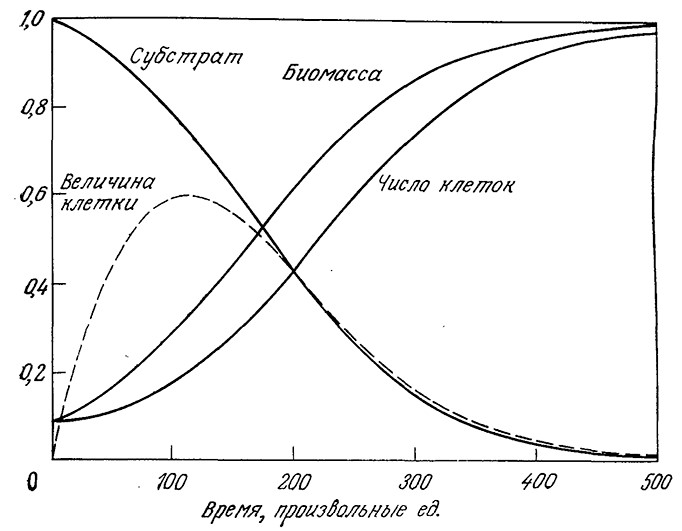
РИС. 7.22. Моделирование роста популяции клеток с использованием инокулята,
находящегося в стационарной фазе, по Уильямсу. Ординаты показывают изменение
во времени безразмерных параметров: концентрации субстрата (s/s₀), концентрации
биомассы (x/Ys₀), численности популяции {f₂x/Ys₀). Здесь отражено также изменение
во времени относительной массы клетки (–1 + 1/f₂).
(Параметры: k₁=0,0125; k₂ ρ_c=0,025; Y=0,5; x₀=0,05; s₀=1; f₂(0) = 1.)

Обратите особое внимание на то, что изменения во времени плотности популяции по массе и по численности клеток непропорциональны; иными словами, масса индивидуальной клетки зависит от скорости роста и даже от предыстории скорости роста. Аналогичные результаты были получены в ходе детального изучения роста популяций Е. coli и S. cerevisiae [30, 31]. Приведенные данные свидетельствуют о том, что динамику изменений клеточной массы часто можно описать с достаточно хорошим приближением относительно простыми математическими моделями; напротив, расчеты динамики численности популяции более сложны.

На рис. 7.23 схематично изображены некоторые модифицированные варианты описанной выше модели. В двухкомпартментальной модели Хардера и Роуэлса компонент G соответствует ферментам, которые катализируют превращение субстрата в промежуточные соединения, использующиеся при построении биополимеров; составные части клетки характеризуются компонентом К, который образуется из питательного вещества S со скоростью, зависящей от количества G [17]. В этой простой двухкомпонентной клетке взаимопревращение GhK путем полимеризации и деполимеризации отвечает состоянию метаболизма поддержания. Составные части трехкомпонентной клетки (рис. 7.23) характеризуются более четко определенной биохимической природой; здесь К обозначает РНК, G – белок, a R – другие компоненты биомассы [17]. В последнем случае метаболизм поддержания также отражен как кругооборот компонентов K и G.

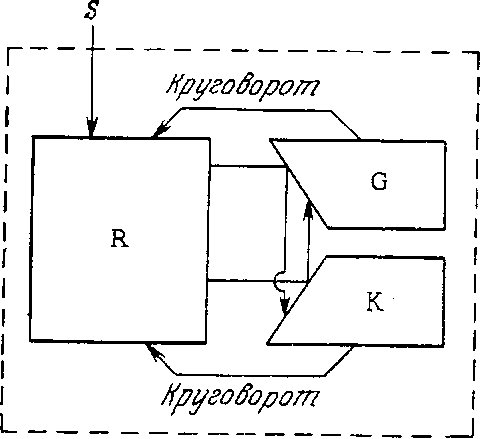
РИС. 7.23. Схемы двухи трехкомпартментальных моделей,
описанных Хардером и Роуэлсом [17].

По сравнению с некоторыми из рассматриваемых ниже более сложных структурированных моделей эти небольшие компартментальные модели относительно просты математически и содержат небольшое число кинетических параметров. Их с умеренным успехом применяли для описания различных состояний несбалансированного клеточного роста. С другой стороны, отсутствие в ряде случаев четкого биохимического определения компонентов затрудняет оценку модели и задачу нахождения параметров. При работе с такими моделями мы не можем воспользоваться известными нам данными о путях метаболизма клетки, регуляции молекулярных процессов и закономерностях клеточного цикла. Эти данные можно применять для моделирования кинетики клеточного роста, только располагая глубоко структурированной моделью клетки, в которой учитывалось бы значительно большее число компонентов, внутриклеточных реакций и взаимодействий.

7.4.2. Метаболические модели

В этом разделе мы рассмотрим и изучим особенности двух различных структурированных моделей кинетики клеточного роста, включающих некоторые стороны клеточного метаболизма. На примере этих моделей мы познакомимся с некоторыми преимуществами и недостатками, свойственными всем более детальным моделям. Эти примеры покажут нам также, что по мере включения в модель все большего числа биологических деталей она становится более специфичной для определенного организма или процесса. При создании метаболической кинетической модели определенной системы необходимо учитывать ключевые детали метаболизма, иногда известные из научных данных или биотехнологической литературы. В известном смысле мы может сказать, что, чем более детализированной становится наша модель, тем больше мы должны знать об изучаемом организме a priori. В противном случае задача выбора кинетических уравнений и значений параметров становится слишком неопределенной, причем неизвестные параметры модели нельзя определить на базе имеющихся (ограниченных) экспериментальных данных. Хотя некоторые из описываемых здесь и других высокоструктурированных моделей, которые мы обсудим позднее, относятся к индивидуальной клетке, обычно принимаемый детерминистический принцип предполагает описание поведения усредненной клетки в большой популяции клеток.

Сначала мы изучим метаболическую модель, разработанную Бийкерком и Холлом [18], а также Памментом, Холлом и Барфордом [19] для аэробного роста почкующихся дрожжей S. cerevisiae. В основу этой модели положены перечисленные ниже допущения, большая часть которых соответствует известным данным о закономерностях клеточного цикла, метаболизма и регуляции экспрессии ферментов организма.

Принятые в модели допущения

1. Индивидуальные изолированные клетки не рассматриваются.
2. Лимитирующий рост клеток субстрат S является одновременно источником углерода и энергии; символом E обозначен этанол.
3. Биомасса состоит из двух частей, А и В.
4. Масса А обеспечивает поглощение субстрата и снабжение клетки энергией, масса В – синтез клеток и их деление.
5. Накопление энергии и продуктов метаболизма происходит в ходе фазы G₁ клеточного цикла, осуществляется массой А и описывается превращением массы А в массу В [см. приведенные ниже уравнения (7.75) и (7.76)].
6. Репликация ДНК, митоз и деление клеток (фазы S, G₂ и М) происходят в течение определенного времени, осуществляются массой В и описываются превращением массы В в массу А.
7. Все участвующие в процессе брожения ферменты сгруппированы и обозначены символом Ef. Аналогично сгруппированы все ферменты дыхательного пути, обозначенные E_r.
8. В каждой ферментной системе биосинтез ферментов регулируется двумя различными путями. Во-первых, ферменты продуцируются со скоростями, пропорциональными интенсивности потока метаболитов, проходящего через эту ферментную систему. Во-вторых, ферменты каждой системы продуцируются еще и в процессе адаптации клетки к изменяющимся условиям; здесь скорость их биосинтеза пропорциональна разности между имеющейся концентрацией фермента и «контрольной» величиной (e_F и e_R  для процессов брожения и дыхания соответственно). «Контрольные» концентрации ферментов пропорциональны интенсивности потока метаболитов, который был бы достигнут при нелимитирующих концентрациях ферментов.
9. Скорости гликолиза и дыхания линейно зависят от e_f/e_F и от e_r/e_R соответственно.
10. Гликолитические ферменты продуцируются в результате работы дыхательного пути (таким путем образуются ферменты для глюконеогенеза, биосинтеза и утилизации внутриклеточных резервных углеводов).

В таком виде клеточный рост можно описать с помощью следующих стехиометрических уравнений [здесь и далее индексами W обозначены переменные, выраженные в единицах массы; в других случаях подразумевается число молей или единиц активности (для ферментов)]:
  

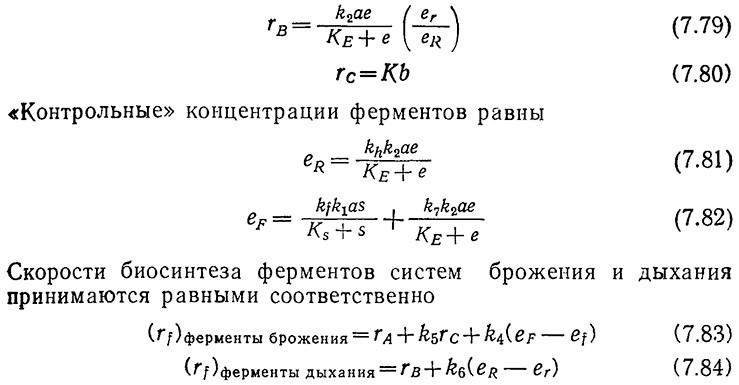
В этих уравнениях символами е_r и e_f обозначены активности ферментов в единице объема культуры. Следовательно, как мы уже упоминали, такая структурированная модель основана не на «собственных» или внутриклеточных концентрациях.

Путем сравнения результатов моделирования и экспериментальных данных по росту культуры дрожжей в периодическом процессе были определены параметры модели, значения которых приведены в табл. 7.3. Применение этой кинетической модели к экспериментам по росту непрерывной культуры в стационарном состоянии потребовало незначительного изменения (от 1,79 до 1,50 в периодическом и непрерывном процессах соответственно) только одного параметра α₃ – экономического коэффициента роста за счет дыхания. Причиной его изменения отчасти послужила известная физиология этого организма, в частности необходимость глюконеогенеза при росте периодической культуры на этаноле и отсутствие такой необходимости при росте проточной культуры на глюкозе (в ПРПП).

Таблица 7.3. Параметры математической модели
роста S. cerevisiae в аэробных условиях^a

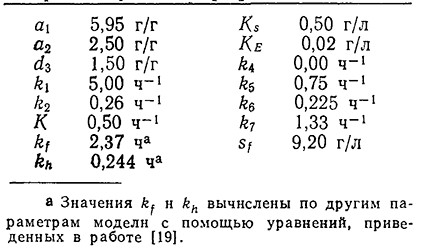
РИС. 7.24. а – рассчитанные путем моделирования зависимости плотности
клеточной массы x (сплошная кривая) и удельных активностей ферментов е_f/х и e_r/х
(прерывистые кривые) от скорости разведения D (ч^–1) для случая роста
непрерывной культуры S. cerevisiae в стационарном состоянии в ПРПП.
Зачерненными квадратиками указаны результаты экспериментального определения х;
б – результаты экспериментального определения удельных активностей ферментов брожения,
NADP⁺-глутаматдегидрогеназы (GluDH– NADP⁺) и алкогольдегидрогеназы (ADH);
в – результаты экспериментального определения удельных активностей ферментов
малатдегидрогеназы (MDH) и изоцитратлиазы (ICL), участвующих в дыхании.

На рис. 7.24, а изображены графики зависимости плотности клеточной массы x(x = a + b) и удельных активностей ферментов брожения (e_f/x) и дыхания (е_r/х) от скорости разведения для случая роста непрерывной культуры 5. cerevisiae в стационарном состоянии; эти зависимости вычислены с помощью параметров, перечисленных в табл. 7.3. Зачерненными квадратиками на этом рисунке обозначены результаты экспериментального определения х, хорошо согласующиеся с расчетными данными. Обратите внимание на то, что здесь зависимость x от D как для экспериментальных, так и для расчетных данных резко отличается от аналогичной упрощенной зависимости, полученной на базе неструктурированной модели Моно (рис. 7.6) На рис. 7.24, б приведены результаты экспериментального определения зависимости удельной активности двух ферментов, участвующих в метаболизме брожения (NADP⁺-глутаматдегидрогеназы и алкогольдегидрогеназы) от скорости разведения в ПРПП. Эти зависимости качественно согласуются с расчетными данными для e_f/х модели. На кривой зависимости удельной активности двух участвующих в дыхании ферментов (малатдегидрогеназы и изоцитратлиазы) от скорости разведения экспериментально обнаружен максимум (рис. 7.24, в); модель предсказывает наличие максимума в зависимости е_r/х от D.

Эти результаты, как и ряд других, приведенных в работе [18], убедительно демонстрируют некоторые из преимуществ, свойственных более структурированному описанию роста популяции клеток. Рассматриваемая модель успешно применялась для описания периодического роста 5. cerevisiae с добавлением субстрата (см. разд. 9.1.1); она также хорошо отражает лаг-фазу в экспериментальных периодических процессах.

В качестве завершающего примера рассмотрим разработанную Шулером и сотрудниками модель индивидуальной клетки Е. сой [24]; из всех предложенных до настоящего времени моделей роста микроорганизмов она наиболее удачна и высокоструктирована. На рис. 7.25 схематично изображены учитываемые в этой модели метаболиты, биополимеры и реакции, осуществляющиеся, как предполагается,, в клетке Е. coli В/r А. Прерывистыми линиями здесь обозначены информационные потоки, регулирующие кинетику реакций. В модель включены реакции образования клеточной оболочки, поэтому продолжительность клеточного цикла является величиной, предсказываемой моделью, а не исходным параметром, как в большинстве других структурированных моделей. Поскольку эта модель разрабатывалась специально для описания роста клеток в условиях ограниченного количества источника углерода или азота, в ней учтеньц многие структурные элементы клетки, участвующие в транспорте и ассимиляции этих веществ. Приведенные на рис. 7.25 реакции учитывают также синтез и утилизацию АТР.

На рис. 7.25 не показаны важные детали модели, связанные с регуляцией инициации синтеза ДНК. В течение очень короткого периода («взрывной синтез») синтезируется белок-репрессор RP; он нейтрализуется белком-антирепрессором ARP, который синтезируется со скоростью, пропорциональной скорости построения клеточной оболочки. При достаточно низкой концентрации RP начинается транскрипция, которая приводит к короткому участку РНК, необходимому для инициации репликации.

К сожалению, объем нашей книги не позволяет описать эту модель достаточно подробно; дополнительные данные читатель может найти в работе [20]. Эта модель включает около 100 стехиометрических и кинетических параметров; почти все эти параметры могут быть определены на основе опубликованных результатов изучения биохимии Е. coli. Насколько велика информация, вложенная в эту модель, настолько же велики и ее возможности.

РИС. 7.25. Схема высокоструктурированной модели индивидуальной клетки, описывающей рост Е. coli В/r А на среде,
содержащей глюкозу и соли аммония.
A₁ – ион аммония; A₂ – глюкоза (и соединения, образующиеся из нее в клетке); W – конечные продукты (CO₂, H₂O и ацетат)
энергетического обмена, выделяемые в процессе аэробного роста; P₁ – аминокислоты; P₂ – рибонуклеотиды;
Р₃ – дезоксирибонуклеотиды; P₄–предшественники клеточной оболочки; M₁ – белки (как в цитоплазме, так и в клеточной оболочке);
M_2RT1 – незрелая «стабильная» РНК; M_2RTM – зрелая «стабильная» РНК (рРНК и тРНК; во всех случаях принимается,
что 85% составляет рРНК); М_2М – матричная РНК; M₃ – ДНК; M₄ – небелковая часть клеточной оболочки
(принимается, что она содержит 16,7% пептидогликанов, 47,6% липидов и 35,7% полисахаридов); M₅ – гликоген; PG – ppGpp;
E₁ – ферменты, участвующие в превращении P₂ в P₃; E₂, E₃ – соединения, участвующие в образовании клеточной оболочки
и регуляции синтеза ее компонентов; GLN – глутамин; E₄ – глутаминсинтетаза; * – вещества, находящиеся вне клетки.

Модель достаточно точно описывает время инициации репликации хромосомы и другие важнейшие особенности клеточного цикла в широком диапазоне скоростей роста. На рис. 7.26 приведены графики зависимости в двойных обратных координатах удельной скорости роста отдельной клетки от концентрации лимитирующего рост питательного вещества (в данном случае иона аммония), полученные экспериментально (точки) и расчетным путем на базе описанной модели (сплошная линия). Обратите внимание на то, что здесь и результаты моделирования, и экспериментальные данные свидетельствуют о существовании нескольких механизмов утилизации иона аммония; это проявляется в изменении наклона при очень больших концентрациях питательного вещества (малых величинах 1/s). Вычисленные путем моделирования закономерности изменения скорости клеточного роста, содержания в клетке гликогена и размера клетки (рис. 7.27) хорошо согласуются с экспериментальными результатами. Рассмотренная нами ранее модель Уильямса предсказывает увеличение размеров клеток при высоких скоростях роста; в отличие от нее описываемая высокоструктурированная модель, учитывающая гораздо большее число биохимических особенностей и деталей метаболизма клетки, показывает, что размер клеток зависит не только от скорости их роста, но и от того, какое питательное вещество лимитирует скорость роста.

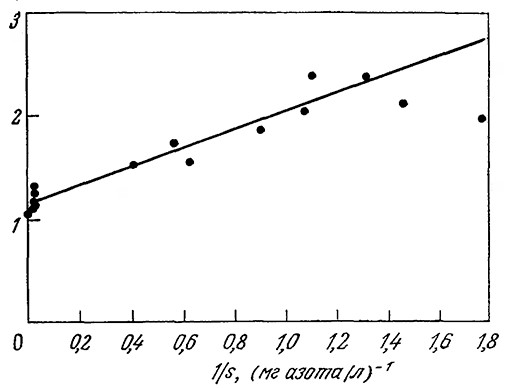
РИС. 7.26. Зависимость удельной скорости лимитируемого источником азота
роста Е. coli В/r А от концентрации иона аммония (сплошная линия –
модельные расчеты; жирные точки – экспериментальные данные).

7.4.3. Моделирование клеточного роста
как оптимального процесса

Изучение роста микроорганизмов на смесях различных субстратов показывает, что обычно организмы быстрее усваивают субстрат, обеспечивающий наиболее высокую скорость роста.

РИС. 7.27. Сравнение результатов, предсказываемых моделью изолированной клетки,
с экспериментальными данными. Приведены расчетная кривая (1) изменения объема клетки
при лимитируемом глюкозой росте (2, 3 – экспериментальные данные); то же (4)
при лимитируемом ионом аммония росте (5 – экспериментальные данные); расчетная кривая (6)
изменения процентного содержания гликогена (7 – экспериментальные данные).

На молекулярном уровне в основе такого поведения микроорганизмов лежат процессы индукции, репрессии, ингибирования и активации, рассмотренные в гл. .3 и 6. Их можно положить в основу соответствующих моделей кинетики роста (разд. 7.5.3), но для этого нужно учитывать множество параметров и детальных сведений о механизме процессов. В альтернативном подходе, разработанном Рамкришной и сотрудниками, влияние регуляторных клеточных процессов описывается как результат оптимизации клеточного роста [21, 22]. В основе этого подхода лежит постулат о том, что в результате естественного отбора и эволюции биологические системы приобрели способность использовать среду оптимальным образом. С точки зрения такой .кибернетической модели действие регуляторных систем метаболизма можно описать как решение задачи оптимального распределения ресурсов, обеспечивающего максимальную скорость роста.

Основанный на законе соответствия для распределения ресурсов алгоритм оптимизации оказался вполне пригодным для моделирования клеточного роста на смешанных субстратах. Если отдача от утилизации ресурса Z_i равна Θ_i(Z_i) и если полная отдача (сумма всех Θ_i) максимизирована при условии», что сумма всех Z_i равна постоянной величине, то должен удовлетворяться следующий закон соответствия:
 

Предположим, что скорость роста популяции зависит от внутриклеточных концентраций е₁ e₂, ….. ряда ферментов, необходимых для ассимиляции субстратов S₁, S₂, …..соответственно. В таком случае, например, вклад субстрата S_i в образование биомассы может быть описан уравнением
   

Весовой коэффициент v_i определяется условиями закона соответствия для энергетического выхода процессов потребления различных субстратов, которые предполагают, что
  
где ν_i – энергия, высвобождающаяся при утилизации единицы массы субстрата j. Применение закона соответствия к распределению клеточных ресурсов для синтеза ферментов приводит к следующему выражению для скорости синтеза фермента E_i:

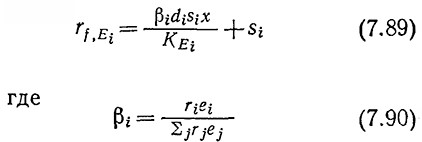
РИС. 7.28. Сравнение экспериментальных (х) и полученных
с помощью кибернетической модели расчетных (---------------)
данных для двухфазного периодического роста Klebsiella oxyloca
в арабинозно-лактозной среде.

Важным преимуществом этой модели является возможность экспериментального определения всех кинетических параметров в реакциях с индивидуальными субстратами. Метод оптимизации учитывает все аспекты кинетики роста популяции микроорганизмов в среде с несколькими субстратами. На рис. 7.28 приведено сравнение расчетных и экспериментальных данных по росту культуры бактерии Klebsiella oxyloca в среде, содержащей арабинозу и лактозу. Соответствующие параметры модели, определенные в отдельных экспериментах, можно найти в работе [22]. В данном случае модель хорошо отражает продолжительную лаг-фазу между периодом роста на лактозе и периодом более медленного роста на арабинозе. Изучение других моделей этого класса показало, что расчетные и экспериментальные данные не только качественно, но и количественно хорошо согласуются и в случае трехфазного роста микроорганизмов на трех субстратах, как в периодическом процессе, так и в стационарной и переходной фазах непрерывного процесса в ПРПП. Большой интерес представило бы распространение кибернетического подхода на другие методы оптимизации и процессы образования продуктов жизнедеятельности клеток. Кибернетические модели являются интересной альтернативой моделей, в которых метаболизм рассматривается как упрощенная сеть химических реакций.