Кинетика образования популяциями клеток продуктов метаболизма может быть описана аналогично росту клеточных популяций. Здесь также возможны структурированный и неструктурированный подходы. Как мы увидим в разд. 7.5.3, модели кинетики белкового синтеза можно разработать и на молекулярном уровне, если воспользоваться известными в настоящее время данными по регуляции молекулярных процессов.

7.5.1. Неструктурированные модели

Кинетика образования продуктов жизнедеятельности клеток наиболее проста в тех случаях, когда образование метаболитов и утилизация субстрата или клеточный рост связаны простым стехиометрическим отношением. Тогда скорость образования продуктов метаболизма можно выразить следующими уравнениями: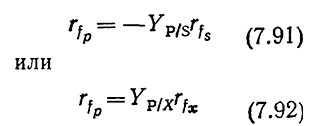
  
соответственно. Такие случаи типичны для микробиологических процессов типа I, рассмотренных в разд. 5.10.3. Примером может служить спиртовое брожение, кинетика которого в периодическом процессе отражена на рис. 7.29. Такого типа кинетику образования продуктов жизнедеятельности иногда называют сопряженной с ростом.

Во многих микробиологических процессах, особенно если речь идет о вторичных метаболитах, продукт жизнедеятельности клеток не образуется в сколько-нибудь значительных количествах в первых фазах периодического процесса вплоть до начала стационарной фазы или даже несколько позже, как, например, процесс биосинтеза пенициллина (рис. 7.30). Иногда в таких случаях кинетика образования продукта жизнедеятельности клеток удовлетворительно описывается простой, не сопряженной с ростом моделью, в которой скорость образования метаболита принимается пропорциональной не скорости роста клеток, а их концентрации.

В ставшей классической работе Льюдикина и Пайрета, посвященной изучению молочнокислого брожения в присутствии бактерии Lactobacillus delbruekii, было показано, что в кинетику образования продукта метаболизма вносят вклад как сопряженные, так и не сопряженные с ростом факторы:
   

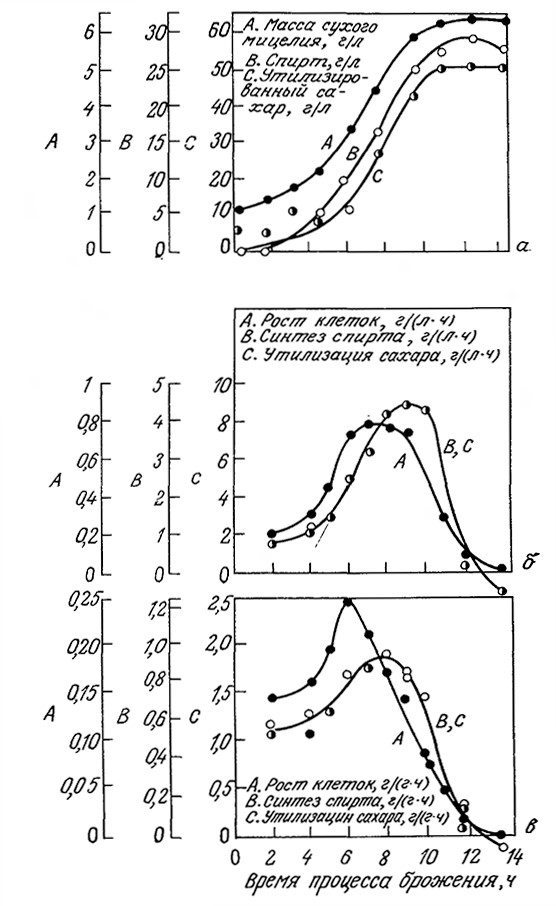
РИС. 7.29. Для процесса спиртового брожения характерна простая сопряженная
с клеточным ростом кинетика образования продукта метаболизма.
На рисунке указано изменение во времени биомассы, массы образовавшегося спирта
и утилизированного сахара (а); объемных и удельных скоростей образования биомассы,
утилизации субстрата и синтеза продукта метаболизма (спирта) (б, в).

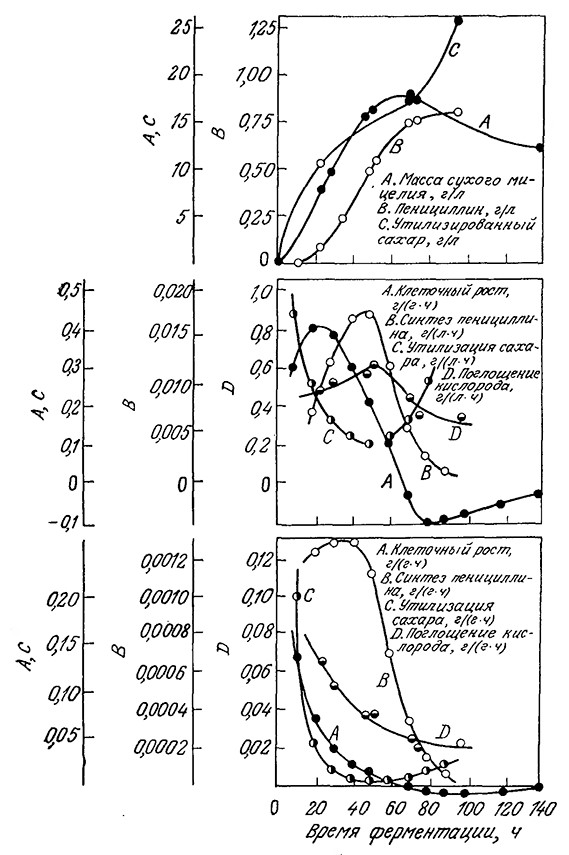
РИС. 7.30. Усложненная кинетика биосинтеза вторичного метаболита пенициллина.
Указано изменение во времени биомассы, массы образовавшегося пенициллина
и утилизированного сахара (а); объемных и удельных скоростей образования биомассы,
синтеза пенициллина, утилизации сахара и кислорода (б, в).

Такое уравнение скорости образования продукта метаболизма с двумя параметрами, часто называемое уравнением Льюдикина – Пайрета, оказалось чрезвычайно полезным при интерпретации экспериментальных результатов самых различных микробиологических процессов. Именно такую форму зависимости следует ожидать тогда, когда изучаемое вещество является конечным продуктом метаболического пути, связанного с выделением энергии (например, в некоторых процессах анаэробного брожения). В этих случаях первое и второе слагаемые правой части уравнения (7.93) можно рассматривать как меру энергии, расходуемой на клеточный рост и на поддержание клеток соответственно.

Таблица 7.4. Классификация микробиологических процессов по Дейндоерферу^a

Временная зависимость концентрации продукта метаболизма в ходе периодического процесса может быть очень сложной, причем в среде могут накапливаться и подвергаться дальнейшим превращениям несколько веществ. Различные возможные ситуации отражены в классификации микробиологических процессов, предложенной Дейндоерфером (табл. 7.4). В некоторых случаях сложная кинетика образования продукта жизнедеятельности клеток может отражать изменения в механизме метаболизма клетки. Показательным примером (важным как с точки зрения промышленного использования, так и в историческом аспекте) такой кинетики может служить синтез ацетона и бутанола бактерией Clostridium acetobutylicum (рис. 7.31). В первой фазе периодического процесса глюкоза превращается в уксусную и масляную кислоты, которые впоследствии перерабатываются (наряду с глюкозой) в ацетон и бутанол. Образование продуктов метаболизма клетки может сопровождаться также химическими превращениями метаболитов в среде, как, например, при спонтанном гидролизе пенициллина. Описание кинетики таких сложных процессов может потребовать включения этих дополнительных реакций в схему математической модели.

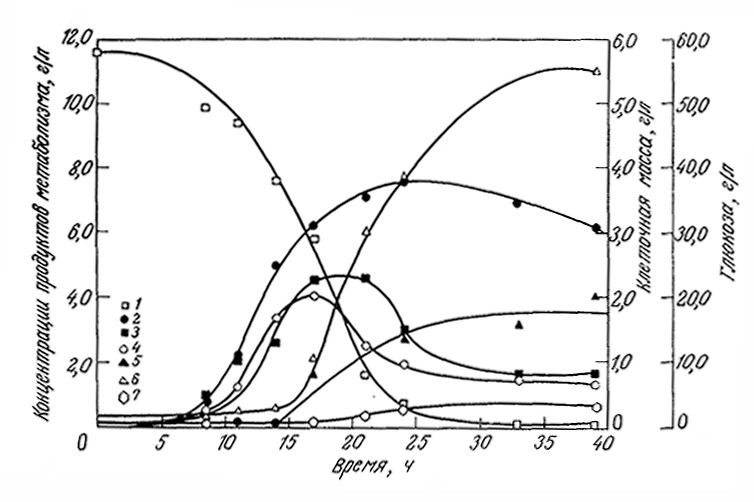
Рис. 7.31. Образование различных веществ в ходе периодического роста Cl. acetobutylicum
при рН 5; приведены экспериментально найденные концентрации глюкозы (1),
клеточной массы (2), уксусной кислоты (3), масляной кислоты (4), ацетона (5), бутанола (6), этанола (7).

7.5.2. Химически структурированные модели кинетики
образования продуктов жизнедеятельности клеток

В сравнении с изучением кинетики роста индивидуальной клетки и популяций клеток в проблеме кинетики процессов образования продуктов метаболизма разработке структурированных моделей посвящено относительно небольшое число работ. Можно ожидать, однако, что развитие структурированных моделей клеточного роста в ближайшем будущем потребует разработки ряда таких моделей. В этом разделе мы рассмотрим интересный процесс образования одного из множества вторичных метаболитов, на примере которого познакомимся с рядом важных аспектов процессов микробиологического синтеза антибиотиков, а также с новыми подходами к моделированию кинетики таких процессов.

Синтез ряда микробных антибиотиков и других продуктов вторичного метаболизма ингибируется высокими концентрациями фосфатного иона. Поскольку для роста клеток фосфат совершенно необходим, очевидно, должен существовать некоторый оптимальный уровень его концентрации. Действительно, такой оптимальный уровень начальной концентрации фосфата наблюдался, например, при биосинтезе алкалоидов Claviseps purpurea (рис. 7.32).

Приведенные на рис. 7.32 экспериментальные данные хорошо моделируются следующими уравнениями кинетики клеточного роста периодической культуры и образования продукта жизнедеятельности [26].

Рост клеток: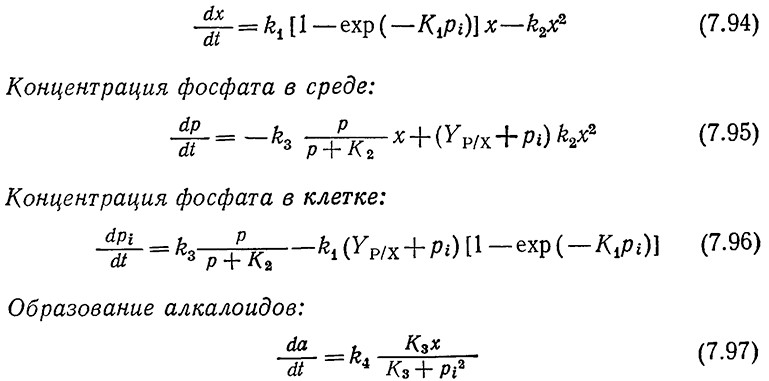
  

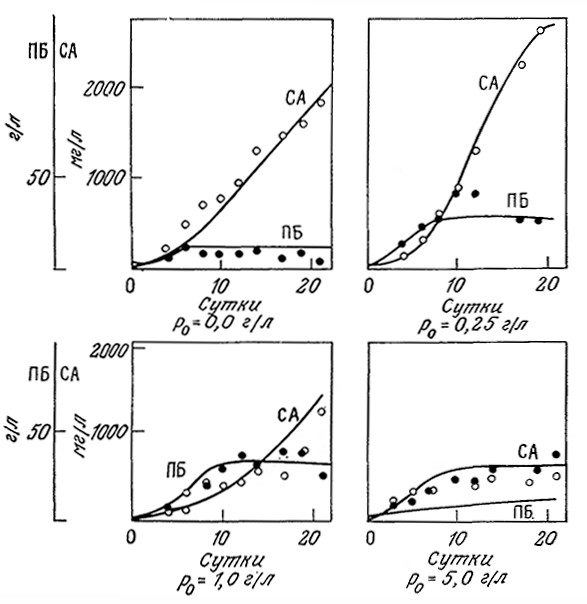
РИС. 7.32. Изменение во времени плотности биомассы (ПБ) С. purpurea (•, г сухого вещества в I л)
и суммы продуцируемых алкалоидов (CA) (О, мг/л) при различных начальных концентрациях фосфата.
Кривые отражают соответствующие расчетные данные, полученные
с помощью описанных в тексте математических моделей.

В этой модели удельная скорость роста описывается уравнением Теиссье, в котором одной из независимых переменных является внутриклеточная концентрация фосфата p_i. (Эта переменная равна числу граммов КН₂РО₄, содержащемуся в 1 г биомассы, и отражает состав клетки. Все другие переменные этой модели, описывающие компоненты системы, измеряются в граммах на 1 л культуры.) Выражение k₂x² отражает скорость лизиса клеток.

В результате лизиса фосфат выделяется в среду; как показывает второе слагаемое правой части уравнения (7.95), его количество пропорционально содержанию фосфата в клеточной массе Y_р/x и внутриклеточной концентрации фосфата р_i. Первое слагаемое той же части того же уравнения описывает активныный транспорт фосфата в клетку; кинетика этого процесса характеризуется наличием режима насыщения. Уравнение материального баланса по внутриклеточному фосфату [уравнение (7.96)] является вариантом уравнения (7.67); здесь учтено, что скорость его образования равна разности между скоростью транспорта фосфата в клетку и скоростью включения фосфата в компоненты клетки. В уравнении скорости образования продуктов принято во внимание ингибирование процесса фосфатом в том виде, в каком этот эффект учитывался ранее при моделировании репрессии фермента фосфатазы.

Таблица 7.5. Значения параметров в структурированной модели кинетики биосинтеза алкалоидов в С. purpurea^а

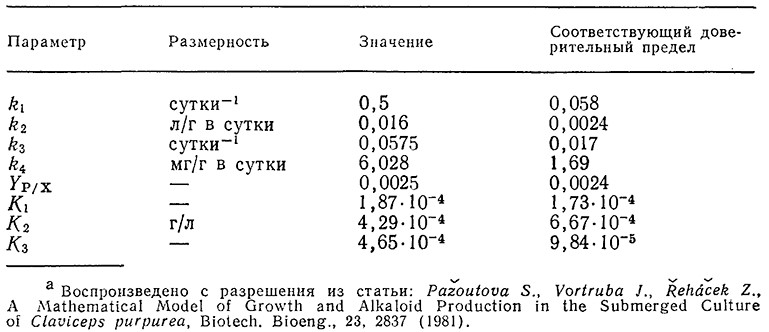
Сплошные кривые на рис. 7.32 были вычислены с помощью описанной модели, а значения соответствующих параметров перечислены в табл. 7.5. Эта структурированная модель хорошо отражает закономерности изменения биомассы и массы алкалоидов во времени, в том числе наличие максимума на кривой накопления суммы алкалоидов, но в то же время при высоких концентрациях фосфата ее точность недостаточно высока. С помощью такой модели, в частности, было показано, что максимальное количество суммы алкалоидов продуцируется при начальной концентрации фосфата в среде 0,17 г/л. Математическое моделирование различных методик введения фосфата (в том числе добавления фосфата по частям в различные фазы процесса) показало, что таким путем нельзя добиться существенного повышения выхода алкалоидов по сравнению с обычным периодическим процессом при оптимальной начальной концентрации фосфата в среде. В других случаях, которые мы рассмотрим в последующих главах, периодические процессы с добавлением субстрата оказываются очень полезными.

7.5.3. Моделирование кинетики образования продуктов метаболизма
на основе механизмов молекулярных превращений;
генетически структурированные модели

Чем точнее описание кинетики в моделщ отражает действительно осуществляющиеся в клетке химические события, тем более универсальной становится наша модель. Здесь под «универсальностью» мы понимаем возможность получения удовлетворительных результатов в условиях, отличающихся от используемых в ходе разработки модели и определения ее параметров. Механизмы белкового синтеза, имеющего большое значение в производстве ферментов, гормонов и других практически важных полипептидов, изучены настолько глубоко, что становится возможной разработка моделей на уровне молекулярных событий и взаимодействий. Подобные модели должны быть в высшей степени универсальными и полезными в оптимизации параметров среды и генетической природы организма.

Материальный баланс по мРНК, образующейся при транскрипции данного гена G, можно выразить следующим уравнением (здесь квадратные скобки служат для обозначения молярных концентраций данного компонента в клетке, выраженных в молях в единице объема клетки):
 

В этом уравнении k_p – константа общей скорости транскрипции, a k_d–константа скорости инактивации и(или) деструкции мРНК; допускается, что оба последних процесса имеют первый порядок. В уравнении (7.98) учтен также коэффициент эффективности утилизации промотора η, отражающий модуляцию транскрипции оператором. Во многих случаях, представляющих практический интерес, оценка η в единицах концентраций белка-эффектора и индуктора или репрессора является наиболее важным этапом всего моделирования.

Аналогично можно записать и уравнение материального баланса по внутриклеточному продукту трансляции, т. е. по исследуемому белку:
  

Здесь скорость синтеза белка пропорциональна концентрации кодирующей данный белок мРНК и эффективности ее утилизации на рибосомах (можно достаточно обоснованно предположить, например, что изменение пуклеотидиой последовательности в связывающем рибосому центре приведет к изменению величины ξ). В этом случае мы опять принимаем, что реакция инактивации белка имеет первый порядок.

При сбалансированном росте производные от [мРНК] и [Р] по времени равны нулю, и при этом условии из уравнений (7.98) и (7.99) следует, что
  

Это уравнение непосредственно выражает концентрацию внутриклеточного белка через параметры, характеризующие экспрессию гена и мРНК, а также стабильность белка в клетке.

Таблица 7.6. Значения^a параметров модели кинетики экспрессии генов в Е. coli^б

В табл. 7.6 приведены характерные средние значения параметров описанной модели для синтеза белка в Е. coli, отражающие найденные зависимости параметров скоростей транскрипции и трансляции от скорости роста.

Имеющиеся в настоящее время данные свидетельствуют о том, что во многих случаях скорость экспрессии генов в Е. coli лимитируется стадией транскрипции. Следовательно, скорость экспрессии регулируемого оператором гена зависит от эффективности транскрипции этого гена, которая в свою очередь определяется совместным влиянием модулирующих агентов на сайты оператора и связывания РНК-полимеразы. В качестве примера рассмотрим систему промотор-оператор гена Iac Е. coli, причем основное внимание будем уделять совместному влиянию lаc-репрессора, индуктора и ДНК на экспрессию гена и, следовательно, на β-галактозидазную активность [28].

Количество продуцируемого фермента пропорционально эффективности утилизации промотора η, которая в свою очередь пропорциональна вероятности того, что операторный сайт О не связан с белком-репрессором R. Таким образом,
  
Здесь [О]₀ – общая концентрация операторных сайтов в клетке Е. coli. Дробное выражение в правой части уравнения (7.101) можно определить, если учесть взаимодействия между R, О, другими неспецифическими сайтами ДНК (D), индуктором I; предполагается, что все эти взаимодействия равновесны: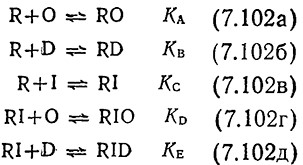
  

Оператор О может существовать в трех различных формах, концентрации которых можно связать следующим уравнением материального баланса:
[O]₀=[O] + [RO] + [RIO]      (7.103)

Аналогично уравнение материального баланса по R можно записать в виде
[R]₀= [R] + [RI] + [RO] + [RD] + [RIO] + [RID]      (7.104)

Поскольку концентрация [D] неспецифично связывающих сайтов ДНК выше общей концентрации R, мы можем принять, что
[D]≈[D]₀      (7.105)

Используя приближение (7.105), равновесную природу реакций (7.102), уравнение материального баланса (7.104) и пренебрегая членами с множителем [O]₀/[R]₀, нетрудно прийти к следующему уравнению: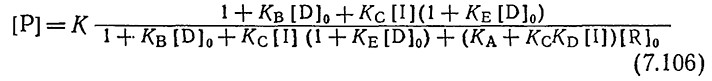
   

Опубликованные в литературе экспериментальные данные позволяют приближенно, с точностью не ниже одного порядка величин, оценить параметры этого уравнения [28]:
[D]₀ = 4•10^–2 M     K_A = 2•10¹²  M^–1
K_B = 1•10^–3 M^–1     K_c = 2•10⁷  M^–1               (7.107)
K_D = 2•10⁹ M^–1     K_E = 1,5•10⁴  M^–1

 Оценка параметров этой математической модели требует обширных экспериментальных данных, но вместе с тем моделирование с учетом молекулярных взаимодействий имеет и свои преимущества. Так, ее параметры имеют строгое физико-химическое толкование и часто могут быть определены в отдельных экспериментах in vitro. Более того, модель такого уровня обладает особой характеристикой, называемой генетической структурой. Под генетической структурой в данном случае понимается четкая зависимость определенных параметров модели от генетической природы; так, изменение нуклеотидной последовательности /ас-оператора должно сопровождаться изменением параметров K_A и К_D, характеризующих взаимодействия Iacоператора с белком-репрессором. По мере развития и углубления наших знаний о механизмах взаимодействий в системе ДНК–белок, вероятно, мы сможем учитывать влияние определенных изменений нуклеотидной последовательности на соответствующие константы связывания ДНК с белком расчетным· путем. Тогда разработанная на молекулярном уровне кинетическая модель позволит осуществлять картирование нуклеотидной последовательности, отражающее продуктивность популяции клеток. Потенциальные возможности такого подхода для рациональной количественной оптимизации генетической модификации организма (или, по меньшей мере, клонированных участков ДНК) очевидны.

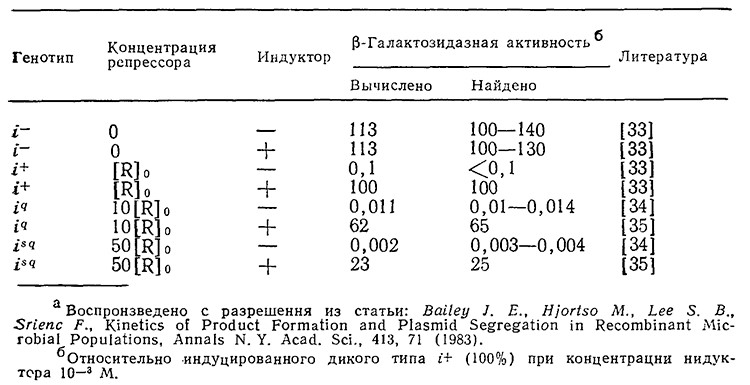
В качестве примера рассмотрим применение уравнения (7.106) для расчета влияния концентрации репрессора на скорости индуцированной и неиндуцированной транскрипции Iacпромотора-оператора хромосомы Е. coli. Необходимые экспериментальные данные, в том числе внутриклеточные концентрации репрессора для каждого из мутантов, известны для мутантных штаммов i^–, i^q и i^sq Ε. coli. Эти величины можно непосредственно использовать при моделировании; они не влияют на другие параметры модели. Как показано в табл. 7.7, модель удовлетворительно отражает влияние внутриклеточной концентрации репрессора как в присутствии индуктора, так и без индуктора. В приведенной в конце главы литературе можно найти другие примеры моделирования с учетом регуляции на молекулярном уровне.

Таблица 7.7. Вычисленные и найденные экспериментальным путем величины β-галактозидазной активности,
регулируемой системой lас-промотор-оператор, для дикого типа Е. coli и трех мутантов (i^–, i^q, i^sq)
с различными внутриклеточными концентрациями lас-репрессора R ([R]₀ = 2•10^–8 М)^а

7.5.4. Кинетика образования продуктов жизнедеятельности
филаментозными организмами

Кинетика образования продуктов метаболизма и утилизации субстрата плесневыми грибами и другими филаментозными организмами обычно очень сложна. Типичным примером может служить биосинтез пенициллина в периодическом процессе. Как показано па рис. 7.30, существуют три различных режима усвоения субстрата. В течение первых 20 ч происходит быстрая утилизация сахара, сопровождающаяся активным ростом плесени. В стационарной фазе утилизация субстрата замедляется, а скорость образования пенициллина достигает максимума. Затем скорость усвоения сахара опять возрастает и удерживается на высоком уровне вплоть до его истощения.

Аналогичная картина наблюдается и в ходе биосинтеза других антибиотиков, хотя каждый процесс имеет и свою специфику. В производстве стрептомицина, например, максимальная скорость синтеза антибиотика достигается (по сравнению с пенициллином) позднее, а заключительная фаза ускоренной утилизации сахара не наступает вообще. Процесс продуцирования антибиотика окситетрациклина филаментозным микроорганизмом Streptomyces rimosus интересен тем, что здесь результат всего процесса зависит и от морфологии организма. В табл. 7.8 суммированы основные стадии и особенности этого процесса.

Таблица 7.8. Основные фазы периодического процесса биосинтеза окситетрациклина
в погруженной культуре Streptomyces rimosus^a

Ниже перечислены некоторые особенности образования продуктов жизнедеятельности, характерные только для филаментозных организмов и найденные экспериментальным путем:

1. Максимальный выход продукта метаболизма достигается в определенной фазе периодического процесса при условии оптимальной начальной концентрации субстрата. Повышение концентрации субстрата приводит к ускорению роста, но при этом субстрат расходуется в основном на образование биомассы, а метаболит синтезируется в очень малых концентрациях. Если же концентрация субстрата слишком низка, то образующееся незначительное количество биомассы не в состоянии синтезировать антибиотик в достаточных концентрациях даже в период максимальной скорости его биосинтеза.

2. Образование продукта метаболизма максимально при минимальном ветвлении активно растущих гиф инокулята. С другой стороны, уменьшение степени ветвления повышает продолжительность лаг-фазы и, следовательно, длительность всего процесса. Очевидно, должна существовать некоторая оптимальная степень ветвления гиф инокулята.

3. Поскольку плесени и другие мицелиальные микроорганизмы являются аэробами, казалось бы, что максимальная интенсивность перемешивания погруженной культуры должна способствовать эффективному переносу кислорода к плесени и, таким образом, росту последней. В случае пенициллина, однако, было установлено, что максимальные выходы антибиотика достигаются при некоторой промежуточной интенсивности перемешивания. Этому факту было дано несколько объяснений. Известно, что на морфологию плесени влияют механические воздействия; возможно, что более энергичное перемешивание способствует ветвлению гиф, которое, как считается, снижает скорость биосинтеза антибиотика. Не исключено также, что существует некоторая оптимальная скорость подачи кислорода, но ввиду сложности системы подтвердить это предположение экспериментальным путем чрезвычайно трудно. (Влияние перемешивания мы рассмотрим подробнее в гл. 8.)