Примерные температурные кривые отдельных слоев корки и мякиша приведены на рис. 72.

График, приведенный на рис. 72, показывает, что температурные кривые мякиша ассимптотически приближаются к температуре 95—98° (температура испарения t_ис).

Это некоторое понижение t_ис против 100° (несмотря на присут­ствие в хлебе солей и кислот) мо­жет происходить вследствие того, что: 1) барометрическое давление ниже 760 мм ртутного столба, 2) влага мякиша в значительной степени свя­зана адсорбционно-осмотическими силами. Давление насыщенного пара таким образом связанной воды меньше давления пара свободной воды, поэтому t_ис≤100°.

Передача тепла к свободной поверхности корки происходит конвекцией и л t_ис≤100°|нием. Для плотности теплового потока q (количество тепла, вос­принимаемого свободной поверхностью корки в единицу времени на единицу поверхности) можно написать:

Из формулы (7) видно, что α есть функция t_n, но для небольших интер­валов изменения t_n можно считать коэфициент α постоянным.

Задача нахождения температур­ного поля выпекаемого теста-хлеба связана с решением диференциального уравнения Фурье для образца неправильной геометрической формы при изменении его агрегатного состоя­ния (испарение влаги из корки с по­степенным углублением зоны испаре­ния, а также и изменением объема образца в первом периоде выпечки).

Поэтому точное решение такой задачи невозможно. Для приближенного ре­шения задачи воспользуемся методом Льюиса, который разработал его для задач диффузии.

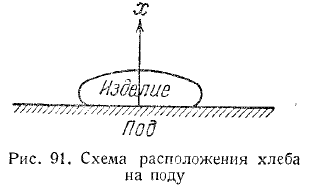
Решим задачу для второго периода процесса выпечки, когда объем образца теста-хлеба не изменяется. Образец лежит на иоду (случай выпечки подового хлеба). Распределение температуры в направлении х (рис. 91 и 92) В верхней и нижней корке принимаем за линейное, а в мякише за параболическое. Так как прогрев не симметричный, то распределение температуры в мякише описывается двумя параболами, которые сопрягаются между собою вершинами. В самом общем случае общая вершина сопряжения переме­щается в направлении х, т. е. R_n= f(т). Толщина нижней корки £^нк не равна толщине верхней корки £^вк

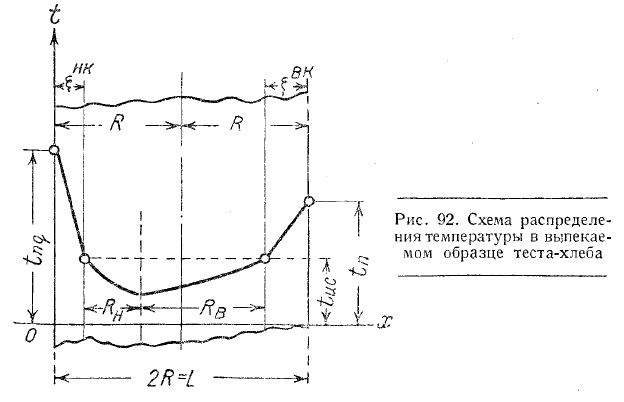
Температура поверхности верхней корки изменяется с течением времени t^bk = f(т), а температура поверхности нижней корки равна температуре пода t_пд. На границе раздела корки-мякиша температура все время одинакова и равна температуре испарения t_ис= 95—98°=const.

Обозначим индексом ^вк данные для верхней корки, индексом ^нк — для нижней и индексом ^мяк для мякиша. Тогда распределение температуры в корке будет таково:

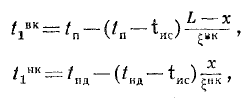
Верхняя корка во втором периоде процесса выпечки образуется за счет удаления влаги в окружающую среду, т. е. закон изменения от времени — здесь закон прямой:

Нижняя корка образуется за счет термовлагопроводности, поэтому тол­щина этой корки увеличивается по закону параболы, т. е.

Таким образом, распределение температуры в нижней корке находится по уравнениям (9) и (11) однозначно.

Чтобы найти зависимость между температурой и временем для верхней корки, надо знать закон изменения £^вк_п от времени, т. е. найти вид функции t^bkn=f(т)

С этой целью воспользуемся граничным условием, которое можно на­писать так

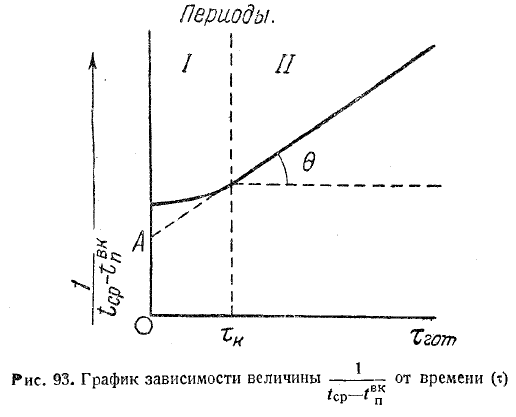
т.е. зависимость между величиной, обратной £ср—t^вк_п и временем, должна иметь вид прямой (рис. 93). Это дает возможность по экспериментальной кривой t^вк_п= f(т) определить необходимые параметры α и £_твп [коэфициент b₂ определяется из кривой кинетики выпечки, см. формулу (5)].

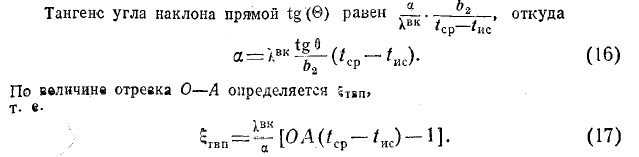
Температуру поверхности корки обычно не определяют, а замеряют тем­пературу елоя корки на некоторой глубине h = L — х; поэтому экепериментальная кривая температуры £хв к= f ( т ) относится к определенной точке

Пользуясь соотношениями (8) и (14), находим уравнение такой температурной кривой

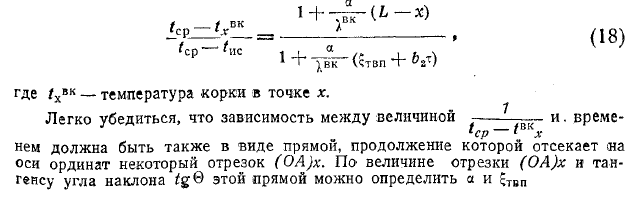
Таким образом, зависимость между температурой выпекаемого продукта и временем выпечки определяется соотношение между t^вк_п и т.

Для практических расчетов можно полагать £^нк = £^вк — 0, т. е. вели­чиной £^нкможно пренебречь по сравнению с L.

Как видно из уравнений (18—23) для аналитического определения темпе­ратуры выпекаемого теста-хлеба в любой его точке и в любой момент вре­мени выпечки необходимо знать термические коэфициенты корки и мякиша в отдельности.

Можно вывести приближенное уравнение для определения температуры мякиша, в которое будут входить только термические коэфициенты мякиша, определение которых представляет меньшие трудности по сравнению с опре­делением термических коэфициентов корки.

При выводе этого уравнения сделаем с целью упрощения задачи следую­щие допущения: 1) температура поверхности (зоны) испарения по всей поверх­ности образца хлеба одинакова и равна t_ис = const., 2) толщина корки (и верхней и нижней) ничтожно мала по сравнению с размерами образца, так что ею можно пренебречь. Тогда для второго периода процесса выпечки можно написать:

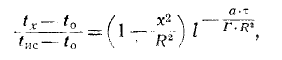
Как видно из уравнения (24), для определения температуры в любой точке мякиша (t_х) необходимо знать из переменных коэфициентов только коэфициент температуропроводности мякиша.