Идея метода. По этому методу вблизи исходной точки («фона») ставится специальным образом спланированная небольшая серия опытов, в которой одновременно варьируются все изучаемые факторы, каждый на 2 уровнях (верхнем и нижнем). Результаты этих опытов математически обрабатывают для получения приближенного математического описания процесса в этой локальной области. Для двух уровней варьирования факторов можно найти только линейное уравнение, величина факторов входит в первой степени (его иногда называют уравнением регрессии). В уравнение могут входить также коэффициенты при S₁S₂, S₂S₃, S₁S₃ и так далее – мультипликативные члены, учитывающие межфакторные взаимодействия.

Уравнение используют для определения направления крутого восхождения, при котором возрастает выходной показатель P наиболее круто, по градиенту. Так происходит до тех пор, пока уравнение адекватно процессу. Что когда-нибудь оно станет неадекватным, очевидно, раз процесс имеет оптимум в виде «хребта» или «купола».

Поэтому по методу Бокса – Уилсона в направлении крутого восхождения ставят 5–6 поверочных экспериментов с ожидаемым возрастанием величины P9 рассчитанной по уравнению. В какой- то точке при экспериментальной проверке этих опытов происходит снижение параметра оптимизации (вслед за его повышением в предыдущих точках).

Поскольку микробиологические процессы сложны и плохо воспроизводимы, планируемые опыты не приводят сразу к «тотальному» оптимуму. Поэтому в наилучшей достигнутой точке ставят новую серию «изучающих» экспериментов, и цикл крутого восхождения повторяется.

Графически данная процедура представлена на рис. 7.5.

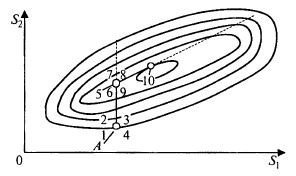
Рис. 7.5. Процедура оптимизации по методу Бокса–Уилсона

Точки 1, 2, 3 и 4 представляют собой начальную серию исследовательских экспериментов вокруг исходной среды А. Их математический анализ дает уравнение, по которому определяют направление крутого восхождения (градиента), показанное на рисунке сплошной прямой, перпендикулярной к топографическим линиям поверхности отклика. Проверочные точки на прямой не представлены, указана только точка «перевала» при движении в этом направлении (точка 5), после которой значение выходного показателя начинает уменьшаться.

В этой точке проводят новую серию опытов 6, 7, 8 и 9, их обрабатывают, находят новое уравнение и по нему вновь ставят эксперименты в направлении крутого восхождения (прямая между точками 5 и 10). В точке 10 достигнуто новое значение оптимума, уже весьма близкое к «тотальному». Линии крутого восхождения до «перевала» изображены сплошными, после – пунктирными. Поскольку для метода Гаусса – Зайделя и крутого восхождения на графике показана одна и та же поверхность отклика, из графика отчетливо видно преимущество метода Бокса – Уилсона: всего за два «прохода» удалось получить близкий к оптимальному результат.

Далее рассмотрим технику применения метода Бокса – Уилсона, в которой математические процедуры планирования опытов и расчетов чередуются с определенным образом поставленными экспериментами.

Исследовательская серия опытов. Как уже указывалось, сначала ставится небольшая серия опытов на двух уровнях – верхнем и нижнем. Для каждого фактора эти уровни отличаются от основного уровня (исходного уровня «фона») на одну и ту же величину.

Эта величина называется интервалом варьирования и обозначается λ. Для разных факторов величина λ может быть разной.

Выбирают интервалы варьирования на основе предварительных данных о процессе, а проще говоря, на основе интуиции исследователя. Не следует брать слишком большие интервалы варьирования: в них может «спрятаться» сам оптимум и исказить всю картину. Лучше выбирать небольшие интервалы, но так, чтобы разница между выходным показателем процесса P для верхнего и нижнего уровней изучаемого фактора была заметной (с учетом возможных погрешностей измерения и вариабельности процесса).

Обычно степень влияния разных факторов на результат процесса различна. Поэтому и 'интервалы варьирования для разных факторов, как правило, различаются.

Для чего ставится исследовательская серия опытов? Чтобы получить линейное уравнение, связывающее выходной параметр оптимизации P с влияющими факторами:

P= b₀ + b₁S₁ + b₂S₂ + b₃S₃ +... + b_nS_n.      (7.1)

В этом уравнении S\, S2, S3, Sn- значение уровней соответствующих факторов; Ьь Ь2, Ь3, ..., bn – соответствующие линейные коэффициенты; Ь0 – также коэффициент, свободный член.

Итого необходимо найти (n + 1) коэффициентов для процесса с числом факторов n.

Значит, минимальное-число опытов в исследовательской серии не может быть меньше (n + 1).

Однако для более точного определения направления крутого восхождения (т. е. более точного математического описания процесса) лучше иметь большее число экспериментов, учитывая погрешности анализов и плохую воспроизводимость микробиологических процессов.

Кроме того, для упрощения расчетов по методу Бокса–Уилсо на опыты ставят не при произвольным образом измененных значениях уровней разных факторов, а по так называемым ортогональным матрицам.

В этих матрицах (а проще, перечне вариантов, взятых в данной исследовательской серии опытов) из всех возможных 2ⁿ вариантов опытов, когда η факторов варьируется на 2 уровнях, выбрано небольшое количество вариантов со следующими свойствами:

1. в каждой серии количество вариантов опытов с верхним уровнем каждого фактора равно количеству вариантов с нижним уровнем того же фактора;

2. верхний уровень любого фактора сочетается одинаковое число раз и с верхними, и с нижними уровнями всех остальных факторов, он как бы проверяется на усредненном фоне, в котором влияние уровней остальных факторов нивелируется. Это же положение справедливо и для нижних уровней.

Такие ортогональные матрицы обязательно имеют число вариантов планирования, кратное четырем (4, 8, 12,16, 20, 24, 32 и т. д.).

Планы ортогональных матриц разработаны для различного числа факторов n и могут включать разное число вариантов планирования. Практически в исследовательских сериях стараются уменьшить число вариантов опытов. Для этого целесообразно выбрать ближайшую матрицу с числом вариантов большим, чем (n + 2).

Планы экспериментов имеются в различных справочниках и руководствах.

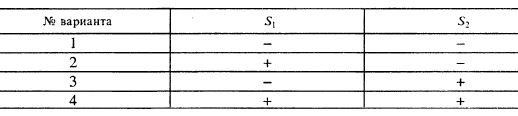
Для n = 2 это, очевидно, полный факторный эксперимент, где взяты все возможные сочетания нижнего и верхнего уровней двух факторов (табл. 7.1.)

Таблица 7.1. Матрица планирования для 2 факторов на 2 уровнях

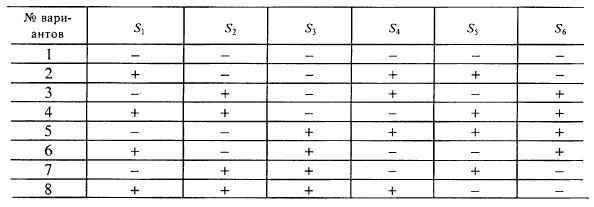
Матрица планирования для 6 факторов на 2 уровнях (табл. 7.2), состоящая из 8 экспериментов, может быть использована также для 3 факторов (это – полный факторный эксперимент), для 4 и для 5 факторов (вычеркивая за ненадобностью 1, 2 или 3 столбца из этой матрицы).

Таблица 7.2. Матрица планирования для 6 факторов на 2 уровнях

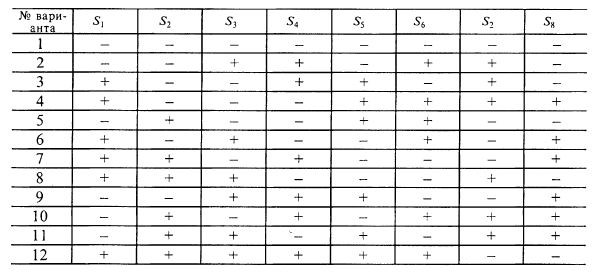
Аналогичным образом может быть использована также матрица для 8 факторов на 2 уровнях из 12 опытов (табл. 7.3).

Таблица 7.3. Матрица планирования для 8 факторов на 2 уровнях

Обычно при планировании эксперимента редко варьируют число факторов больше 8. Поэтому и в исследовательских матрицах редко используют число опытов больше 12 или в крайнем случае 16.

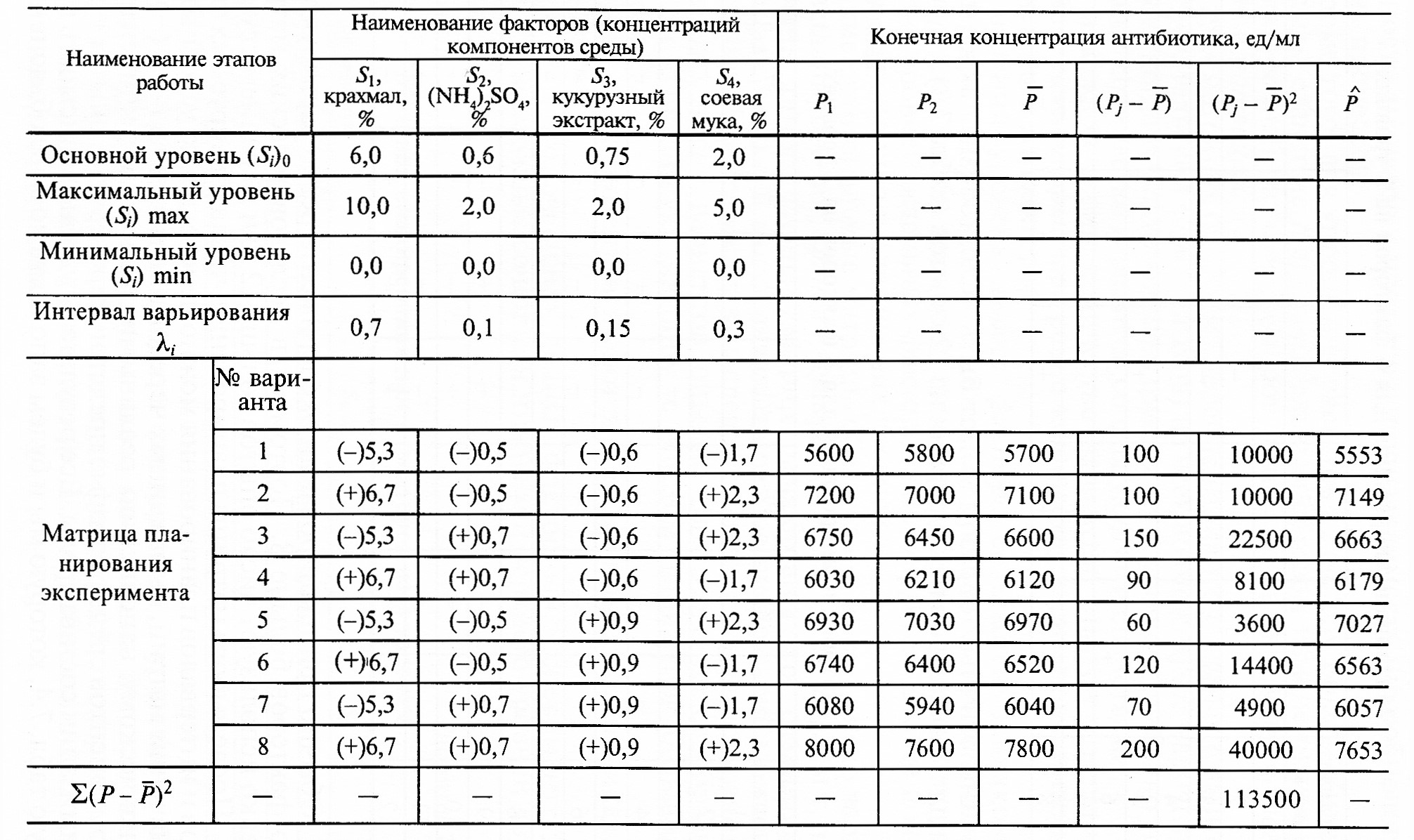
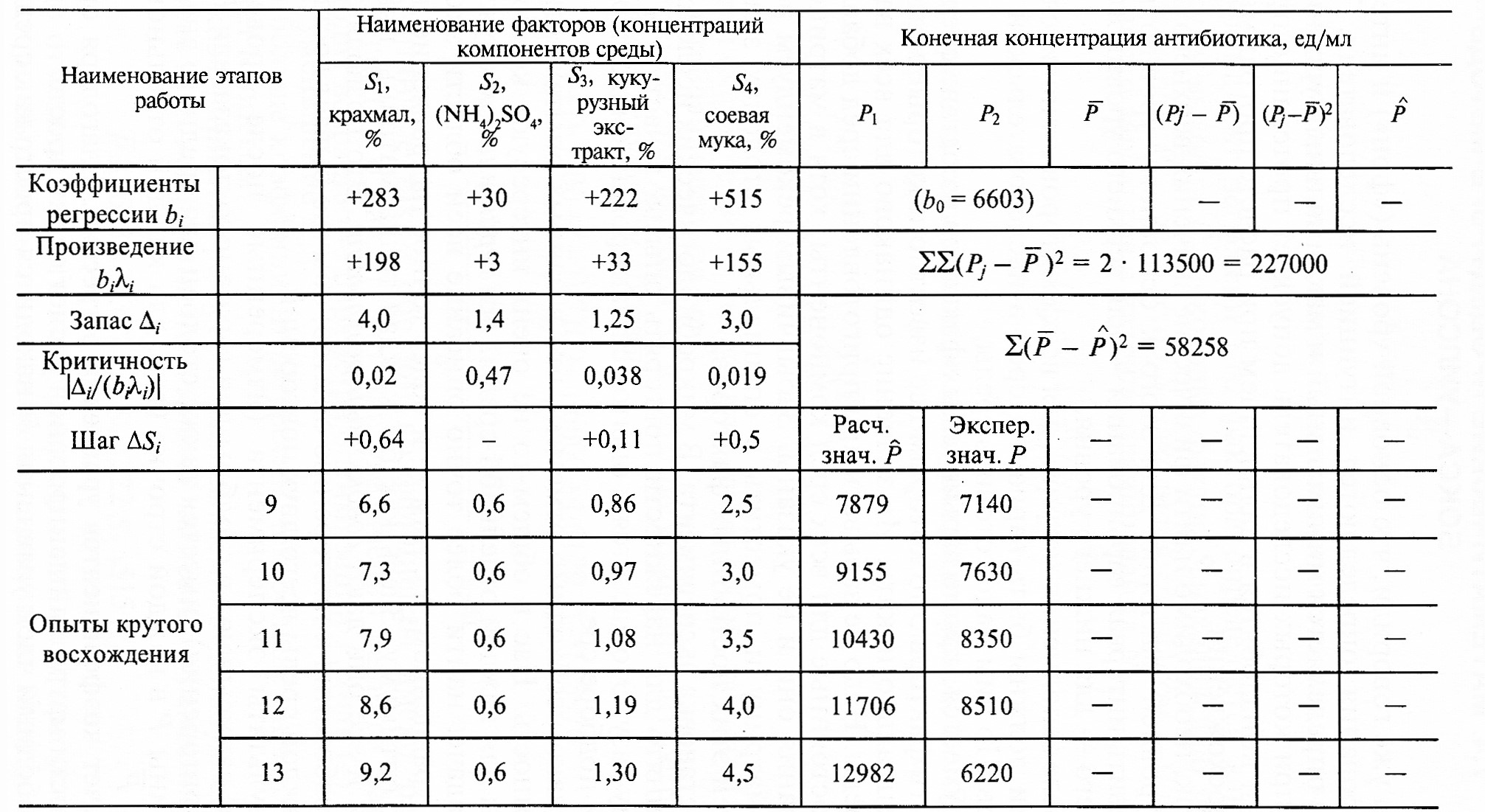
После выбора матрицы планирования, числа варьируемых факторов и интервалов планирования можно переходить от условных обозначений матриц, выраженных чередованием знаков (-) и (+), к их физическому наполнению реальными значениями концентраций компонентов среды, которые предстоит проверять в опытах при оптимизации состава среды. Все результаты удобно записывать в сводную табл. 7.4, которую мы и будем заполнять по мере объяснений.

Таблица 7.4. Пример оптимизации 4-компонентной среды по методу Бокса–Уилсона