Мы уже говорили, что основной уровень («фон») и интервалы варьирования определяются интуицией исследователя. Точно так же определяется минимальный и максимальный уровни фактора, при которых исследователь допускает протекание процесса. Они понадобятся в дальнейшем при расчете программы крутого восхождения.

Итак, необходимо найти физические значения верхнего и нижнего уровней факторов. Для этого к основному уровню нужно прибавить интервал варьирования – для верхнего уровня или вычесть его – для нижнего уровня.

После заполнения матрицы для всех факторов становится ясно, какими должны быть варианты сред в исследовательской серии опытов. По ним надо готовить среды.

Разумеется, кроме варьируемых факторов в составе среды могут быть факторы, по которым все известно и которые нет смысла специально искать. Их значение одинаково для всех вариантов среды. Надо не забывать при приготовлении сред добавлять и эти постоянные для всех сред компоненты, хотя в матрице планирования они и не указаны. Забывчивым рекомендуем расширить матрицу и поместить в специальных столбцах значения уровней этих постоянных факторов.

Постановка эксперимента. В микробиологических исследованиях принято для надежности повторять опыты, зачастую и не по одному разу. Это касается и опытов с планированием эксперимента при подборе сред.

Однако необходимо отметить, что в данных опытах есть одна особенность. Нас в общем-то не очень интересуют конкретные цифры для каждой отдельной среды. Вся серия в целом служит одной задаче: найти более точно описание всей области эксперимента уравнением, а с ним – и более точное направление движения к оптимуму. Здесь как бы каждая точка матрицы помогает другой и все они дают совокупный результат. Это позволяет снизить требования к повторению опытов; обычно бывает достаточно для каждой среды всего двух повторений.

Результаты эксперимента (измеренные после проведения опыта) записывают в столбцы для выходного показателя Р₁ и P₂ (два повторения), имеется также столбец для среднего значения величины P в каждой строчке (т. е. для каждой отдельной среды) – Р̅.

Расчет коэффициентов уравнения регрессии. Благодаря ортогональности матрицы планирования расчет очень прост.

Свободный член уравнения b₀ находится просто как среднее из значений P для всех N вариантов матрицы: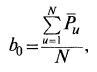
(7.2)
где P̅_u – среднее значение величины P для всех повторений для u-го варианта матрицы.

Коэффициент регрессии i-го фактора определяется как разность сумм выходов P̅_u, в которых фактор S_i находился со знаком (+), и выходов P̅_u, где фактор Si находился со знаком (-), деленная на число вариантов в матрице планирования N: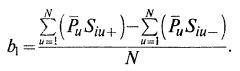
(7.3)

Если принять кодированные значения факторов X_i, т.е. S_iu, как (+1) для верхнего уровня и (–1) для нижнего, то получаем: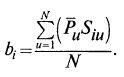
(7.4)

В этой формуле знаки получаются сами собой, так как вычисляется алгебраическая сумма.

Например, для фактора S₂ в таблице коэффициент регрессии вычисляют следующим образом: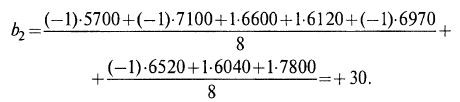

Рассчитанные таким образом коэффициенты имеют разные знаки. Знак (+) означает, что при увеличении данного фактора происходит возрастание параметра оптимизации P, знак (-) – наоборот, уменьшение Р.

Чем больше коэффициент регрессии, тем больше он влияет на результат процесса.

Все коэффициенты регрессии записываем в отдельную строку. На основе этих коэффициентов можно записать и уравнение

P̅ = 6603+283 S₁+30 S₂+222 S₃+515 S₄

Надо отметить, что эти коэффициенты найдены при условии, что факторы выражены в масштабе кодированных коэффициентов. Чтобы перейти к натуральным переменным, нужно подставить выражение для кодированных факторов:
     (7.5)
где S̅_i и S̅_0i – натуральные значения уровня i-го фактора в данном опыте и основного уровня этого фактора; λ_i – интервал варьирования i-го фактора в натуральных величинах (в кодированных величинах это 1).

Для расчета программы крутого восхождения используют коэффициенты регрессии в натуральных величинах (b_i λ_i). Запишем строчку этих произведений для всех факторов.

Определение запаса для движения в направлении крутого восхождения. При определении программы крутого восхождения от основного уровня необходимо знать для каждого фактора запас Δ, в сторону движения [для коэффициентов регрессии со знаком (+) – в сторону увеличения, со знаком (–) – в сторону уменьшения]:
Δ_i = S_{i max} – S_0i если b_i > 0 или S_0i – S_{i min}, если b_i < 0.      (7.6)

Отдельная строчка для этого показателя записана в табл. 7.4.

Определение вспомогательного показателя «критичность». Этот показатель представляет собой модуль отношения запаса Δ_i и произведения b_iλ_i и физически выражает в сравнительном аспекте, сколько сможет уместиться в «запасе» шагов в направлении крутого восхождения для разных факторов с учетом их степени влияния на результат процесса. Чем ниже значение показателя критичности для фактора, тем меньшее (по сравнению с другими) число шагов уместится в «запасе» для этого фактора.

Выбор шага крутого восхождения. Обычно крутое восхождение проводится путем равномерного пошагового приращения в каждом последующем опыте величины уровня фактора. При этом для одного из факторов – наиболее критичного – величина приращения (шага) выбирается, а для всех остальных – рассчитывается так, чтобы их значения были пропорциональны произведениям b_iλ_i. При этом надо учитывать и знак приращения: для некоторых факторов с каждым новым шагом необходимо величину фактора увеличивать, для других – снижать, чтобы получить максимально крутое возрастание параметра оптимизации.

Обычно выбирают относительно немного шагов в направлении крутого восхождения: 5–8, не более. По наиболее критичному фактору выбранное количество шагов т позволяет определить и величину шага ΔS_i:
  (7.7)
Здесь ΔS_б – шаг базового фактора.

Обычно эту величину округляют. Надо отметить, что в отличие от коэффициентов регрессии шаг ΔS_i определен уже в натуральных величинах, так что его можно сразу прибавлять (или отнимать) к исходным уровням факторов.

Запишем строчку для вычисленных значений ΔS_i в нашем примере.

Критичным оказался фактор 4, для него выбрано число шагов, равное 6, и шаг оказался равным 

Пропорционально произведениям b_iλ_i найден шаг ΔS_i для факторов S_i: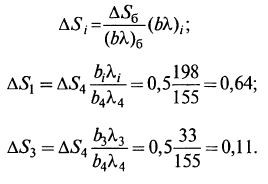
(7.8)

Для фактора S₂ в табл. 7.4 вместо ΔS₂ проставлен прочерк. Это связано с тем, что по результатам анализа установлено, что данный фактор не оказывает существенного влияния на результат процесса, а потому его значение пока что нет смысла менять. Но как определить, что тот или иной фактор является значимым или незначимым? Для этого в планировании эксперимента предусмотрена специальная процедура.