Дисперсия воспроизводимости процесса. В биологических процессах, как нигде, результат процесса обычно неоднозначен. Существует какой-то уровень колебаний, возможных по случайным причинам. Природа этих колебаний (источников неоднородности) может быть различной. Это и ошибки в определении результата, и различия в значении факторов при проведении эксперимента, и неточности приготовления сред, и вообще присущая биологическим объектам неоднородность.

А поскольку коэффициенты регрессии определяют по значениям выходного показателя, то и для них есть какой-то уровень случайных изменений, который и следует найти с помощью статистической обработки.

Уровень воспроизводимости процесса характеризуется дисперсией. Для определения дисперсии воспроизводимости существуют два способа.

Первый способ – многократное повторение опытов для одного и того же варианта (среды). В этом случае имеем ряд значений Pi их количество обозначим γ, оно не должно быть меньше 8–10. Нужно найти среднюю величину P для всех γ опытов, все отклонения от среднего (P-P̅), квадраты этих отклонений и сумму квадратов
  для всех γ повторений.

Дисперсию воспроизводимости определяют по формуле: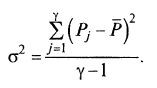
 (7.9)

Это не среднеквадратичное отклонение, а именно дисперсия воспроизводимости каждого отдельного измерения.

Интересно, что средняя величина P̅ колеблется значительно меньше, чем каждое отдельное измерение. Если, например, выполнить несколько серий опытов на одной и той же среде (в каждой серии число опытов у), затем для каждой серии рассчитать свою среднюю величину P̅, а потом посмотреть, какова будет дисперсия воспроизводимости для этих средних значений, то получим:

Ơ²_p = Ơ²/γ      (7.10)

Второй способ – расчет дисперсии процесса по данным повторных экспериментов матрицы планирования. Он более удобен при планировании эксперимента, так как повторения в каждом варианте матрицы предусмотрены. Если γ – число повторений в каждом варианте среды, a N – общее число вариантов сред в матрице, то дисперсию воспроизводимости единичного значения находят по формуле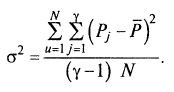
    7.11

Надежность вычисления дисперсии воспроизводимости определяется количеством «лишних» опытов, необходимых для нахождения дисперсии (если γ = 1, то дисперсию воспроизводимости по любой из формул найти невозможно). Это количество «лишних» опытов называют числом степеней свободы f Для первого способа оно равно (γ – 1), для второго – N (γ – 1). Эта величина является важным статистическим показателем и будет использована в дальнейшем.

Необходимо отметить, что для надежного определения дисперсии воспроизводимости процесса число степеней свободы/должно быть не менее 5–8.

Чем больше дисперсия, тем хуже воспроизводимость процесса. Корень квадратный из дисперсии воспроизводимости процесса называют стандартным отклонением, или стандартной ошибкой.

И последнее замечание по второму способу определения дисперсии воспроизводимости. Очевидно, что в разных вариантах матрицы планирования величина выхода P может быть различной: одна среда плохая, другая хорошая. А разброс данных мы принимаем как бы одинаковым (раз все квадраты отклонений для разных сред мы объединяем и находим по существу усредненное значение дисперсии воспроизводимости). Но ведь и уравнение мы ищем усредненное для всего изучаемого диапазона. Так что такое допущение вполне приемлемо.

В табл. 7.4 мы для определения^дисперсии воспроизводимости добавили поэтому столбцы (P_u – Р̅) и (P_u –P̅)², из которых находится сумма квадратов отклонений и дисперсия.

Определение значимости коэффициентов регрессии. Уровень возможных случайных колебаний коэффициентов регрессии называется доверительным интервалом, обозначается буквой ε и его вычисляют по формуле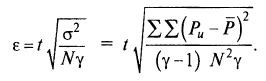
712

В этой формуле появляется новый коэффициент t – критерий Стьюдента, определяемый по таблицам. Для надежности оценки до 95% критерий Стьюдента зависит только от числа степеней свободыf, при которых находили дисперсию воспроизводимости.

Ниже представлены значения критерия Стьюдента для наиболее часто встречающихся значений/при P = 0,95:

Из приведенных данных следует, что вначале критерий t резко уменьшается с возрастанием f, а затем его значение стабилизируется.

Доверительный интервал ε имеет одно и то же значение для всех коэффициентов b_i (в кодированном виде). Сравнение коэффициента регрессии с доверительным интервалом и позволяет сделать вывод о его значимости. Все коэффициенты b_i значения которых ниже доверительного интервала, незначимы. Их можно считать нулевыми. Наоборот, если величина коэффициента больше ε, он значим. При этом, очевидно, имеется в виду модуль коэффициента: отрицательные коэффициенты регрессии тоже значимы, если они по модулю превосходят ε.

Незначимость коэффициентов может быть вызвана различными причинами:

1. взяты слишком малые интервалы варьирования фактора;

2. плохая воспроизводимость процесса – все различия в выходе нивелируются ошибкой опыта;

3. данный фактор находится на уровне, близком к оптимальному;

4. данный фактор не влияет на процесс вообще, по крайней мере в изученной области.

При незначимости каких-то коэффициентов можно увеличить интервалы варьирования по незначимым факторам и повторить эксперимент при новых условиях. А можно не обращать на них внимания, провести крутое восхождение по остальным факторам, и уже в новой матрице изменить интервалы варьирования незначимого фактора.

Так и сделано в данном примере: для незначимого коэффициента при S₂ сохранен уровень фактора, имевший место в основной среде (0,6 %).

Адекватность математического описания процесса. Кроме оценки значимости коэффициентов в процедуре статистического анализа предусмотрена оценка адекватности полученного математического описания в целом. Для этого сначала находят дисперсию адекватности, которая характеризует отклонение рассчитанных по уравнению значений выходного показателя Pˆ от найденного в эксперименте P̅.

Расчетные значения для каждого варианта матрицы можно найти, используя кодированные значения уровней фактора («+» или «-») и соответствующие коэффициенты регрессии.

Например, для варианта 6 (см. табл. 7.4) величину Pˆ можно определить так:

Pˆ = Ь₀ + Ь₁ – b₂ + b₃ – b₄ = = 6603 + 283 – 30 + 222 – 515 = 6563.

Можно найти эту величину Pˆ и для уравнения без незначимого фактора S₂ с коэффициентом b₂.

Pˆ = b₀ + b₁ – b₂ + b₃ – b₄ = 6593.

В табл. 7.4 дан столбец рассчитанных значений Рˆ. Можно добавить еще столбец разностей (Pˆ-P̅), а также столбец квадратов этих разностей (Ρˆ – P̅)². Эти столбцы в таблице отсутствуют, но итог вычислений – сумма квадратов Σ(Ρˆ – Ρ̅)² для всех вариантов сред – приведен в нижней части таблицы.

Дисперсия адекватности определяется по формуле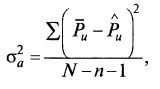
 (7.13)
где n – число факторов в уравнении; N – число вариантов опытов (условий), по которым определяется дисперсия адекватности; u – номер варианта среды, к которому относятся P̅ и Pˆ.

Знаменатель этой дроби представляет собой число степеней свободы f_a дисперсии адекватности
f_a=N–n–1,      (7.14)

т.е. количество «лишних» опытов, имеющихся в плане сверх минимально необходимых (n + 1) – по числу коэффициентов в уравнении. В данном случае f_a = 3 (для примера в таблице).

Степень адекватности математического описания оценивают по критерию Фишера F, который вычисляют по формуле
F = Ơ²_aƴ/Ơ²_p.

В этом уравнении множитель γ в числителе связан с тем, что дисперсия воспроизводимости Ơ_а² определяется не для единичного измерения, а для среднего из γ повторений.

Чтобы найти адекватность уравнения, необходимо критерий Фишера сравнить с табличным F_T, имеющимся в справочниках по статистике, также для надежности оценки 95%.

Уравнение считается адекватным, если F < F_T, и наоборот.

F_T в таблице определяют исходя из двух видов степеней свободы: f_p – для воспроизводимости самого процесса и f_a– для дисперсии адекватности. Искомая величина находится на пересечении столбца для f_a и строки для f_p. Естественно, что дисперсия адекватности Ơ²_a должна быть, как правило, больше дисперсии воспроизводимости Ơ²_p = Ơ²_p/γ, но не больше ее произведения на критерий Фишера.

Строго говоря, лишь при адекватности линейного уравнения принимают решение о крутом восхождении.