Рассмотрим еще один метод математического описания при оптимизации подбора сред.

Этим методом является аддитивно-решетчатое описание процесса. В этом случае объект описывается аддитивно-нелинейным решетчатым уравнением
P= b₀ + f₁[S₁] +f₂[S₂] + ... + f_n[S_n].      (7.17)

Аддитивное –- значит состоящее из суммы членов, каждый из которых зависит только от одного из факторов. Принятое в методе Бокса–Уилсона линейное уравнение регрессии (7.1) тоже было аддитивным, только значения каждой функции были линейными:

f₁(S₁) = b₁S₁;
……………………(7:18)
f_i(S_i) = b_iS_i.

Здесь же функции могут быть и нелинейными, например:
f_i (S_i) = b_iS_i + b_iiS_i² + b_iiiS_i³ + ...       (7.19)

Фактически не обязательно эту зависимость f_i (S_i) описывать каким-то уравнением. Это сразу сужает возможности описания процесса.

Но можно, как это часто делается, описывать зависимость не уравнением, а значениями функции в заданной точке.

На рис. 7.6 представлен пример такой зависимости.

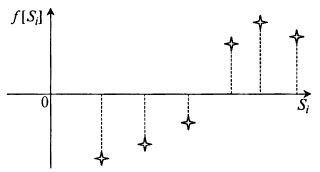
Рис. 7.6. Пример решетчатой функции одного фактора

Здесь значения функцииf[S_i] известны лишь для 6 заранее заданных уровней данного фактора, причем безразлично, какие это уровни и каковы расстояния между ними. Важно только, чтобы они перекрывали интересующий исследователя диапазон изменения факторов и были расположены относительно равномерно внутри этого диапазона.

Таким образом, каждая из составляющих функцийявляется решетчатой, т. е.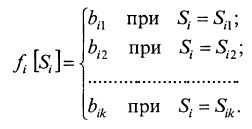
(7.20)

Чтобы получить с наименьшим числом опытов указанные зависимости и упростить вычисления, целесообразно использовать ортогональные матрицы планирования уже не на 2, а на 3, 4, 5 уровнях в соответствии с выбранной разбивкой рабочего диапазона для всех факторов.

Ортогональность матриц, как и в случае с двумя уровнями, предполагает, что каждый уровень любого фактора сочетается одинаковое число раз со всеми уровнями остальных факторов.

На практике такие схемы планирования эксперимента называют схемами ортогональных латинских прямоугольников (или квадратов, если число факторов равно числу уровней каждого фактора).

Есть удобные для практики схемы планирования – 3x3, 4x4, 5 х 5, 8 х 4, 9 х 3. Первая цифра обозначает число факторов, а вторая – число уровней каждого фактора. Число вариантов составляет произведение этих двух цифр, хотя полный факторный эксперимент для такого числа уровней составил бы соответственно 27, 256, 3125, 65536, 19683.

В качестве примера в табл. 7.5 приведен план экспериментов для 4 факторов на 4 уровнях.

Таблица 7.5 Планирование эксперимента для 4 факторов на 4 уровнях

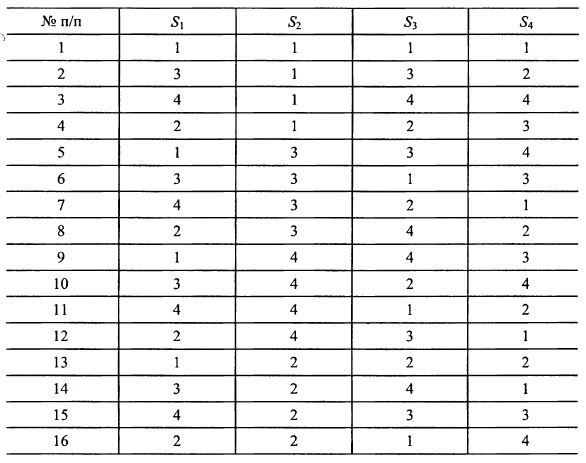
Цифры в схемах соответствуют различным уровням факторов. Но не обязательно, чтобы цифра 1 обозначала наименьший уровень, а цифра 4 – наибольший. Их можно задавать произвольно, важно только потом знать соответствие.

Если требуется изучить меньшее число факторов на том же числе уровней, то в матрице можно отбросить «лишние» столбцы.

Переход от кодированных обозначений уровней к натуральным переменным (концентрациям компонентов среды) проводят аналогично методу Бокса–Уилсона. При этом исследователь принимает значения уровней S_i1, S_i2,…..S_ik для каждого фактора.

Далее опыты ставят с повторениями, аналогичным образом находится среднее значение выхода для каждого варианта среды.

Величина эффектов решетчатого описания (b_ik) и значение Ь₀ рассчитываются почти так же просто, как в методе Бокса– Уилсона: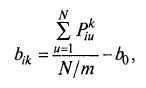
(7.21)  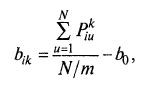               (7-22)

здесь P^k_iu – выход в u-м варианте плана, где i-й фактор находился на k-м уровне; m – число уровней каждого фактора.

В общем нужно найти средний выход P в тех опытах, где вычисляемый фактор находился на определяемом уровне, и вычесть из него средний выход по всей матрице планирования. При этом часть коэффициентов b_ik будет со знаком «+», а часть – со знаком « – ». Для проверки можно использовать соотношение: для каждого фактора алгебраическая сумма b_ik равна 0.

Доверительный интервал для оценки значимости коэффициентов определяется по соотношению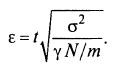
 (7-23)

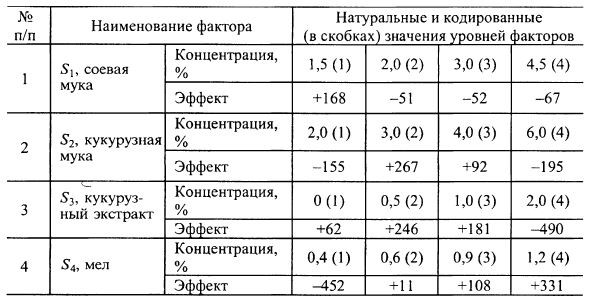
В результате получается довольно наглядная таблица влияния уровней факторов, приведенная здесь для одного из процессов биосинтеза антибиотиков (табл. 7.6).

Среднее значение по матрице составило b₀ = 1635 ед/мл.

Из табл. 7.6 видно, какие уровни факторов обеспечивают наибольший выход антибиотика: 1,5 % соевой муки, 3,0 % кукурузной муки, 0,5 % кукурузного экстракта и 1,2 % мела. Если «собрать» в одной среде эти частные оптимумы по каждому фактору (а среди 16 экспериментов плана такой среды не оказалось), то предсказанное значение выхода составит:

P = 1635 + 168 + 267 + 246 + 331 = 2647 (ед/мл).

Это значение выхода более чем на 50 % превышает исходный уровень, а реально при воспроизведении оно оказалось даже выше (3240 ед/мл).

Адекватность аддитивно-решетчатого описания проверяют аналогично методу Бокса–Уилсона. При нахождении дисперсии адекватности число степеней свободы f_α принимаютf_α = N- n (m–1)–1.

Таблица 7.6 Итоги расчетов величины эффектов аддитивно-решетчатого описания