Одновременно с ростом микроорганизмов или несколько сдвинуто во времени, но в одном и том же процессе ферментации происходит также биосинтез продуктов метаболизма. Закономерности этого процесса также требуют своего математического описания.

Казалось бы, искусственно выведенный математический параметр – удельная скорость роста μ – послужил основой составления многих математических моделей биосинтеза продуктов метаболизма. Собственно говоря, процессы биосинтеза продуктов издавна делили на два больших класса – связанные с ростом и не связанные с ростом микроорганизмов. В качестве примера процессов первого класса можно назвать биосинтез конститутивных ферментов клетки, а второго класса – биосинтез многих антибиотиков, интенсивный синтез которых происходит после прекращения роста микроорганизмов.

Удельная скорость биосинтеза продуктов, связанных с ростом микроорганизмов, может быть выражена простым соотношением
q_P = Kµ,      (8.61)
или
Q_P = KQ_X (K = Y_PX)·     (8.62)

Более сложное выражение было предложено Людекингом и Пайри:
q_Р = q_Р0 + К_µ,     (8.63)
или
 (8.64)

В этом случае часть продукта образуется непрерывно, независимо от роста микроорганизмов, а часть – пропорционально росту.

Есть ряд уравнений, учитывающих нелинейный характер связи q_p и μ:

 (8.65)     (8·66)

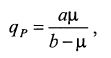
где а и b – коэффициенты.

Эти уравнения дают выпуклую и вогнутую кривые, выходящие из начала координат (рис. 8.21), но могут иметь также дополнительный свободный член рис. 8.22):
   (8-67)            (8-68)

Возможны также эмпирические уравнения типа
q_P = bμ + cμ²     (8.69)
q_P = α + bμ + cμ₂,      (8.70)
где а, Ь, с – коэффициенты (рис. 8.23).

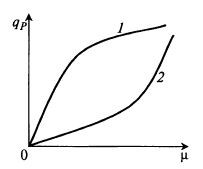
Рис. 8.21. Зависимость q_P(µ) по уравнениям (8.65) и (8.66) – кривые 1 и 2 соответственно

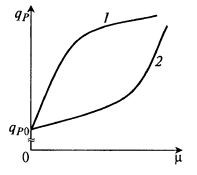
Рис. 8.22. Зависимость q_P(μ) по уравнениям (8.67) и (8.68) – кривые 1 и 2 соответственно

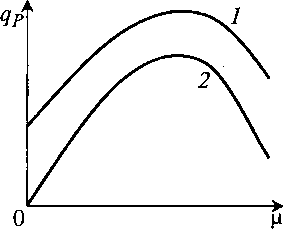
Рис. 8.23. Зависимость q_P(μ) по уравнениям (8.69) и (8.70) – кривые 1 и 2 соответственно