Эти подходы основываются на оценке возрастного состояния популяции клеток.

Если есть измеренная кривая возрастания концентрации биомассы (или клеток) во времени, то в любой заданный момент времени по этой кривой можно определить распределение клеток по возрастам (рис. 8.24).

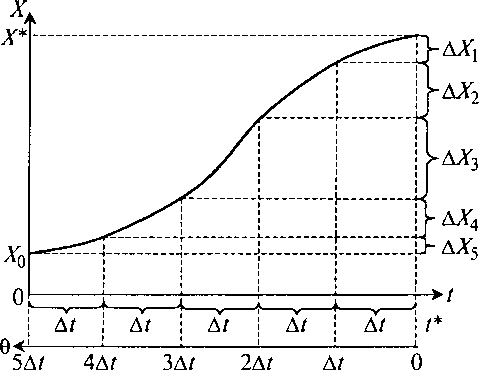
Рис. 8.24. Определение доли клеток разного возраста по кривой роста биомассы:
t – время ферментации; θ – возраст клеток

Откладывая назад от заданного времени промежутки времени Δ t и сравнивая концентрации биомассы в эти моменты времени, мы можем определить, какие количества биомассы в данный момент времени имеют диапазоны возрастов 0 – Δt, Δt – 2Δt, 2Δt – 3Δt, 3Δt – 4Δt, 4Δt – 5Δt и выше – вплоть до времени от начала ферментации t* (табл. 8.1).

Таблица 8.1. Количество биомассы разного возраста в момент времени t*

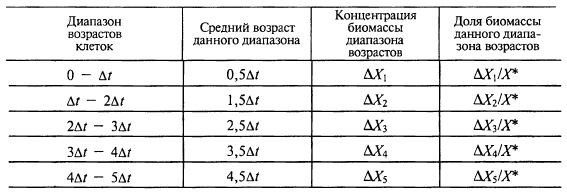
Наблюдаемое в проанализированный момент времени t* значение биосинтеза продукта можно приписать как бы сумме скоростей, привносимых разными фракциями биомассы:
q_P = q₁ΔX₁ + q₂ΔХ₂ + ... + q₅ΔX₅. (8.73)

При этом вполне возможно, что значения q₁, q₂,.., q₅ не будут одинаковыми: «молодежь» не синтезирует нужный продукт, слишком старые клетки – тоже.

Мы рассмотрели, как найти распределение возрастов клеток в популяции микроорганизмов. Это распределение было «подиапа- зонное», т. е. сначала мы задавали произвольно ширину диапазонов возрастов, а затем определяли, какая часть клеток находится в том или ином диапазоне.

Ясно, что уменьшая величину диапазонов Δt до бесконечно малых dt, можно найти распределение клеток по возрастам в виде непрерывной функции распределения Xθ, где θ – возраст отдельных клеток.

Проблемой при учете распределения возрастов является необходимость расчета интегральной скорости биосинтеза продукта q̅_P, которую для некоторого числа поддиапазонов к можно определить по формуле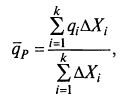
 (8.74)
где ΔX_i – концентрация клеток i-го поддиапазона; k – общее число поддиапазонов.

Очевидно, что  (здесь χ – общая концентрация клеток микроорганизмов).

Переходя к непрерывным функциям, получаем:
q_i = q_iθ, (8.75)
X_i = Χ_i θ. (8.76)

Можно записать выражение для интегральной скорости биосинтеза продукта: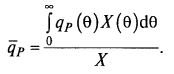
 (8-77)

Вводя обозначения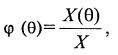
   (8.78)
где ϕ (θ) – плотность распределения клеток по возрасту, получаем: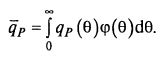
 (8.79)

Ясно, что такой подход к определению только одного показателя несколько сложен, хотя при использовании компьютеров вполне выполним.

Тем не менее для упрощения этого подхода японским исследователем Аибой предложено использовать для оценю* возраста культуры так называемый средний возраст популяции θ̅. Биологически термин вполне понятен – это сумма возрастов всех клеток, деленная на их количество: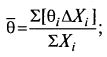
 (8.80)
это величина, отражающая «молодость» или «старость» всей популяции в целом.

Если последовательно уменьшать поддиапазоны Δθ и ΔX, доведя их до бесконечно малых dX и dθ, то для среднего возраста можно получить интегральную формулу: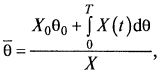
 (8.81)
где X(t) – функция изменения концентрации биомассы во времени; X₀ и θ₀ – начальная концентрация биомассы и ее возраст; T – момент времени, для которого определяем средний возраст культуры.

Представим функцию X(t) графически (рис. 8.25).

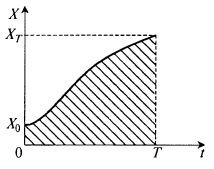
Рис. 8.25. Графическое вы ражение интеграла из уравнения (8.81)

Интеграл в формуле (8.81) численно равен заштрихованной площади на рис. 8.25, так что его нахождение практически очень просто.

В качестве примера можно привести два процесса, представленные на рис. 8.26. В момент времени Гони характеризуются одной и той же концентрацией биомассы X_T, в начале процесса концентрации X₀ у них также одинаковы. И тем не менее мы можем сказать, что культура в процессе 2 имеет меньший средний возраст (более молодая), чем в процессе 1.

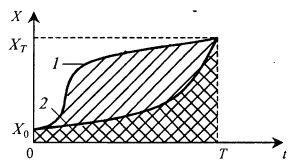
Рис. 8.26. К сравнению возрастных характеристик двух культур микроорганизмов с разной предысторией роста биомассы (кривые 1 и 2)

Это следует из того, что площадь под кривой 2 значительно меньше, чем площадь под кривой 1.

Другое возможное упрощение предлагает определять не полное распределение клеток по возрастам, а, так сказать, ступенчатое. Предполагается, что клетки синтезируют продукт, если их возраст выше некоторой величины θ *, называемой возрастом зрелости (рис. 8.27):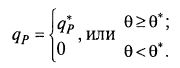
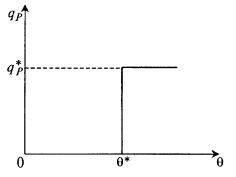
 (8.82)

Рис. 8.27. Графическое выражение уравнения (8.82)

Распределение биомассы по возрастам также ступенчатое, состоящее из двух поддиапазонов: доля клеток с возрастом меньше возраста зрелости (ΔX₁) и, соответственно, больше (ΔX₂) – риc. 8.28.

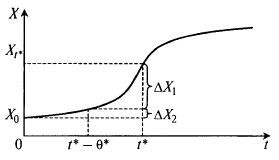
Рис. 8.28. Определение соотношения клеток продуктивного и непродуктивного возраста в заданный момент времени t* по кривой роста биомассы:
X₀ – концентрация биомассы в начале процесса; X₁ – концентрация биомассы в момент времени t*; ΔX₁ – доля концентрации клеток, имеющих возраст в диапазоне О– θ*, т. е. ниже возраста зрелости; ΔX₂ – доля концентрации клеток, имеющих возраст выше θ*, т. е. выше возраста зрелости

По такой схеме при t < θ* получается, что «зрелых» клеток нет вообще, далее они появляются, а доля «незрелых» падает.

Интересно, что в зависимости от роста культура может сохранять свой возраст в течение долгого времени неизменным, «молодеть» или «стареть». Пример представлен на рис. 8.29.

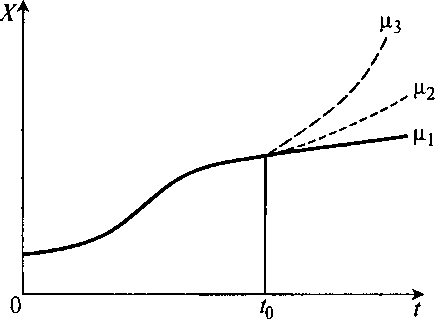
Рис. 8.29. Варианты роста биомассы микроорганизмов после момента времени t₀ при различных μ

В момент времени t₀ культура c некоторой предысторией, определяемой ее средним возрастом θ̅₀, в зависимости от технологических воздействий может начать расти медленно с удельной скоростью роста μ₁, или быстрее – μ₂, или еще быстрее – μ₃.

Для того чтобы возраст культуры не изменялся, должно соблюдаться равенство
μ = 1/θ̅. (8.83)

Допустим, что до момента времени t₀ удельная скорость роста равна μ2:
μ₂ = 1/θ̅. (8.84)
где θ̅₀ – возраст культуры в момент времени t₀

Если μ > 1/θ̅₀, т. е. μ₃ > μ₂ = 1/θ₀, то культура будет «молодеть».

Если же μ < 1/θ̅₀, в данном примере μ₁ < μ₂ = 1/θ̅₀, то культура будет «стареть».

Зная оптимальный средний возраст культуры, мы можем так управлять ростом биомассы, чтобы биосинтез продукта был на максимальном уровне.

Теперь остается рассмотреть форму зависимости биосинтеза продукта q_P от среднего возраста культуры q_P =f(θ̅).

Если зависимость имеет возрастающий характер с насыщением (рис. 8.30), то ее удобно выразить в форме, похожей на уравнение Моно:

 (8.85)        или           (8.86)

Если, наоборот, она убывает с возрастом (рис. 8.31), то лучше подходит выражение, подобное уравнению Иерусалимского: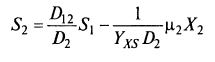
 (8.87)       или           (8.88)

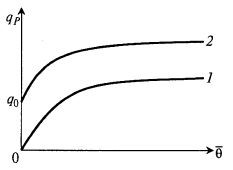
Рис. 8.30. Вариантызависимости q_P(θ̅) с насыщением:
1 – по уравнению (8.85); 2 – по уравнению (8.86)

Часто используется полиномиальная форма зависимости, учитывающая наличие экстремума:
q_P = q₀ + q₁θ̅ + q₂θ̅². (8.89)

Хорошо подходит для многих процессов кусочно-линейная аппроксимация (рис. 8.32) зависимости

 (8.90)

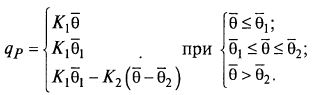
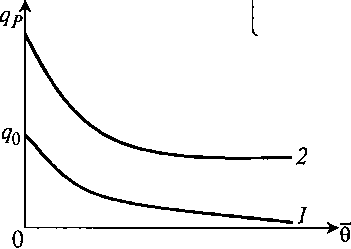
Рис. 8.31. Варианты в зависимости q_P (θ̅):
1 – по уравнению (8.87); 2 – по уравнению (8.88)

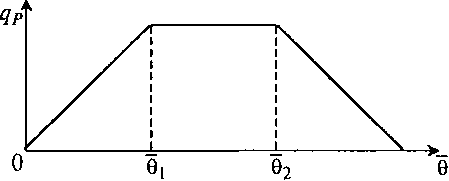
Рис. 8.32. Кусочно-линейная форма зависимости q_P (θ) по уравнению (8.90)

Возможны и другие зависимости в соответствии с характером кривой q_P(θ̅).

Надо отметить, что возрастной подход пригоден и для оценки человеческих популяций, а может быть, он и взят из этой практики.

Часто говорят о старении или омоложении населения города, страны, даже вуза или завода. У нас, например, средний возраст студентов практически мало меняется, зато в последнее время очень увеличился средний возраст преподавателей.