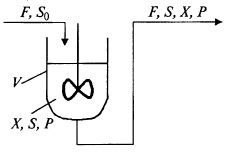
В хемостатном процессе ферментация протекает в аппарате с мешалкой. В аппарат с постоянной скоростью подводится свежая питательная среда; из аппарата непрерывно с той же скоростью отводятся ферментационная среда, содержащая биомассу, продукт метаболизма и остатки субстрата (рис. 9.3).

Рис. 9.3. Схема хемостатного непрерывного процесса ферментации

Предполагают, что в любой точке аппарата и на выходе из него концентрации S, Х и P равны.

Интересно, что на вход в аппарат не подают непрерывно посевной материал. Засев производится единовременно при запуске культуры от периодического процесса, а далее биомасса непрерывно сохраняется в ферментере и специального подсева не нужно.

Для описания закономерностей хемостатного процесса необходима математическая модель, описывающая кинетику процесса.

Примем для простоты следующие допущения:
   (9.3)

μ̃ = 0 (отсутствует диссимиляция биомассы); (9.4)

Q_P= 0 (нет образования продукта метаболизма); (9.5)

Q̃_P = 0 (нет инактивации продукта метаболизма); (9.6)

m_S = 0 (нет затрат на поддержание жизнедеятельности культуры). (9.7)

В этом случае выражение для материального баланса в ферментере записывают следующим образом: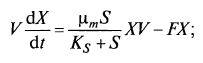
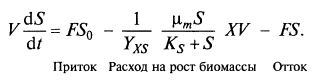
 (9.8)
 (9.9)
Здесь V– объем ферментационной жидкости в аппарате, сохраняемый на постоянном уровне.

Принимаем:
D = F/V, (9.10)
где D – скорость разбавления, ч^–1

Систему уравнений (9.8) и (9.9) можно записать упрощенно: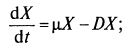
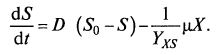
 (9.11)            (9.12)

Введем в уравнение (9.11) вместо μ зависимость μ(S):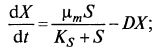
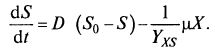
 (9.13)             (9.14)

В отличие от периодического в непрерывном хемостатном процессе довольно быстро устанавливается стационарное состояние, при котором скорость роста биомассы будет равна скорости ее вымывания из аппарата, а скорость притока субстрата за вычетом оттока остаточного субстрата равна скорости его расходования на рост микроорганизмов. При этом
 (9.15)                (9.16)

Решая при этих условиях уравнение баланса биомассы, получаем:
mХ – DX = 0 и μ = D. (9.17)

Итак, в установившемся состоянии удельная скорость роста становится равной скорости разбавления D (это управляемый параметр, его задает оператор).

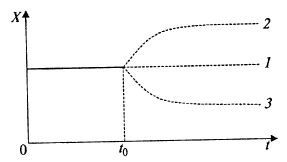
Если в установившемся состоянии в момент времени t₀ по каким-либо причинам μ ≠ D, возникает переходный процесс по биомассе (рис. 9.4).

Рис. 9.4. Переходные процессы, возникающие в непрерывном хемостатном процессе при изменении скорости разбавления или роста биомассы:
1 – исходное состояние культуры и продолже­ние процесса после t = t₀ при μ₁ = D;
2 — пере­ходный процесс при увеличении μ в момент времени t = t₀ при μ₂ > D;
3 — переходный процесс при снижении μ в момент времени t = t₀ при μ₃ < D

Из уравнения (9.11) следует, что если при этом μ станет больше D, то скорость роста биомассы в аппарате dX/dt > 0, и биомасса возрастает (кривая 2 на рис. 9.4). При этом она потребляет из среды больше субстрата, концентрация его снижается, уменьшается и μ. Устанавливается новое равновесие μ = D при большей концентрации биомассы.

Если величина μ станет меньше D, то dX/dt < 0, и концентрация биомассы начнет снижаться и, соответственно, будет возрастать концентрация субстрата. При этом новое установившееся состояние будет при более низкой концентрации биомассы (кривая 3 на рис. 9.4).

Таким образом в хемостате осуществляется саморегулирование.

Эти процессы представлены на рис. 9.4.

Определим теперь концентрацию субстрата и биомассы в установившемся процессе в хемостате.

С учетом (9.17) можно записать:
 (9.18)            откуда  (9.19)            (9.20)

Поскольку μ = D, получаем:
X – Y_XS (S0 S) (9.21)             или   (9.22)

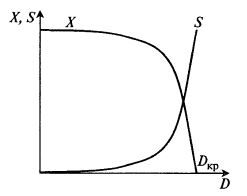
Графические зависимости между установившимися значениями X и S в хемостатном процессе и скоростью разбавления D называют хемостатными кривыми (рис. 9.5).

Рис. 9.5. Хемостатные кривые X(D) и S(D) в стационарном состоянии

Хемостатная кривая X(D) имеет особенность: концентрация биомассы снижается до нуля при повышении скорости разбавления до некоторого критического значения и при более высоких скоростях разбавления остается равной нулю. Физически это означает, что культура вымывается. Выходит больше биомассы, чем может вырасти.

Определим, при каких значениях D_KP происходит вымывание культуры:

 (9.23)               (9.24)

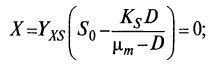
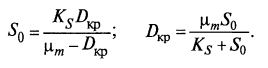
Отсюда следует, что вид хемостатной кривой зависит от S₀. При D = 0
X = YXS S0. (9.25)

Таким образом, и начальное положение хемостатной кривой, и точка вымывания зависят от концентрации субстрата в свежей среде (подпитке) S₀. Эта величина наряду со скоростью разбавления является параметром, с помощью которого оператор может управлять процессом. Чем больше S₀, тем выше концентрация биомассы в выходном потоке, причем в довольно широком диапазоне скоростей разбавления концентрация биомассы сохраняется почти на постоянном высоком уровне, лишь немного снижаясь с возрастанием скорости разбавления.

Интересную особенность имеет зависимость стационарной (остаточной) концентрации субстрата от начальной (входной) его концентрации. В уравнении (9.19) нет ничего, кроме D и кинетических констант µ_m и K_S. Из этого следует парадоксальный вывод: при любом изменении концентрации субстрата во входящем потоке S₀ в стационарном состоянии при заданной скорости разбавления устанавливается одна и та же остаточная концентрация субстрата S. Именно это свойство хемостата дало ему название: концентрация субстрата (химического соединения) стабилизируется сама по себе независимо от колебаний на входе.

Если же говорить о том, что же регулируется оператором извне, то это сама скорость разбавления. Поэтому этот процесс иногда называют «спидостат» (от английского speed – скорость).

Итак, мы знаем, как будут выглядеть кривые X(D). Возникает вопрос: к чему стремиться? Здесь надо снова вспомнить о производительности процесса Q_X (количество биомассы, образующейся в единицу времени единицей объема среды в аппарате). Для непрерывного процесса
Q_X = DX, (9.26)

или после подстановки выражения для X из (9.22):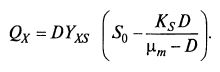
 (9.27)

Как и в периодическом процессе, практический интерес представляет определение условий (в данном случае – скорости разбавления D), при которых величина Q_X будет оптимальной.

Для определения экстремума необходимо приравнять нулю частную производную

откуда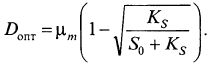
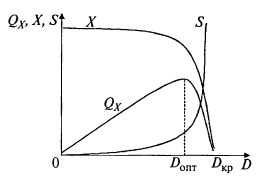
 (9.28)

На рис. 9.6 показано, что производительность по биомассе в хемостатном процессе сначала возрастает до Donj, а затем резко падает.

Рис. 9.6. Зависимость производительности по биомассе Q_X в хемостатном процессе, концентрации биомассы X и остаточной концентрации субстрата в аппарате S от скорости разбавления D

При оптимальной скорости разбавления Dom концентрация биомассы составляет:
 (9.29)

Само же значение оптимальной продуктивности
Q_ОПТ = D_ОПТ X_ОПТ ≈ D_ОПТY_XSS₀ (9.30)

так как величина S<<S₀.