Если в составе среды изучают не один фактор, а два или более, задача усложняется. Например, для двух факторов нужно уже построить поверхность отклика, напоминающую топографическую карту. На этой карте на двух осях координат отложена величина факторов S1 и S2, а в самом графике проведены контурные линии равного уровня, соответствующие одинаковому выходу Р – параметру оптимизации (рис. 7.2).
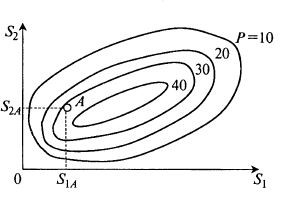
Рис. 7.2. Пример поверхности отклика по концентрации
продукта P для двух компонентов среды (S1 и S2)
На этом рисунке в качестве примера представлены линии равного уровня для величины выходного показателя – 10, 20, 30 и 40. В точке А с координатами S1А и S2A, например, выход является средним между 30 и 40.
Ясно, что для построения такой «топографической карты» нужно «изрешетить» всю площадь в изучаемом диапазоне Si и S2 опытами. Обычно поступают следующим образом.
Выбирают значение фактора S1, а затем для этого значения проводят, например, 5 экспериментов, варьируя фактор S2. Затем берут новое значение S1 и вновь проводят 5 экспериментов, варьируя S2. И так повторяют несколько раз, пока не получится 5 уровней фактора S1, каждый из которых проверен со всеми 5 уровнями фактора S2.
Это можно было бы отразить в виде семейства характеристик P (S2) при разных значениях S1 (рис. 7.3) или наоборот.
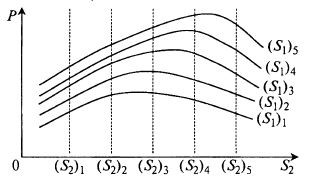
Рис. 7.3. Семейство зависимостей P (S2) при разных значениях S1
Из этого семейства кривых P= f (S2) можно найти максимальное значение выхода. Оно имеет место в точке с координатами S1 = (S1)5 и S2 = (S2)4, хотя, если бы мы «изрешетили» поверхность отклика более часто, можно было бы ожидать чуть больших значений в квадрате между S1 = (S1)4...(S1)5 и = (S2)4…(S2)5. Можно «изрешетить» более часто только этот квадрат и тем самым уточнить оптимум функции P = f (S1, S2).
Ясно, что такой подход к изучению оптимума (а он называется тотальным перебором на прямоугольной сетке) можно распространить и на большее число изучаемых факторов. Правда, графически результат уже представить невозможно: физически существует только трехмерное пространство. Но «изрешетить» гиперповерхность отклика P = f (S1, S2, S3,..., Sn) всегда можно. Если затем поставить в этих точках эксперименты, то при этом выбирается такое сочетание уровней факторов, которое дает наибольшее значение S1.
Попробуем оценить, сколько экспериментов нужно поставить при тотальном переборе для обычного числа факторов в средах (5...8). Если количество уровней каждого фактора выбрать 5, а число факторов тоже 5, необходимо 5•5•5•5•5 = 3125 экспериментов. Для числа факторов 8 число экспериментов будет 390625. Если уменьшить число уровней фактора для более грубого изучения, например до 4, то число экспериментов для 8 факторов будет 65536, а для 4 – 256.
Отсюда следует, что метод тотального перебора на прямоугольной сетке требует довольно большого числа экспериментов.
Поскольку время и деньги у исследователя обычно ограничены, применение такой схемы на практике нерационально. Вот если бы был известен аналитический вид функции P = f (S1, S2,…Sn), то на компьютере такой подход вполне осуществим. Тотальный перебор при хорошем быстродействии там вполне возможен и часто применяется в несложных экстремальных задачах.
Отдельное изучение каждого фактора. Обычно при подборе сред микробиологи применяют исходный «фон» – определенное соотношение уровней факторов (концентраций компонентов) в среде. На этом «фоне» ставят однофакторные эксперименты по каждому из η факторов и получают столько же кривых, сколько изучают факторов. Число уровней, как мы уже говорили, может быть 5–6, так что общее число экспериментов будет 5n или 6n – значительно меньше, чем 5n или 6n. Так, для 5 факторов на 5 уровнях это будет 25 опытов, для 8 факторов на 5 уровнях – 40. Это несоизмеримо меньше, чем при тотальном переборе. Затем находят «локальный» оптимум по каждому фактору (он обычно отличается от уровня фактора в «фоне») и «собирают» как бы оптимальное (квазиоптимальное) значение всех факторов, составленное из этих локальных оптимумов для S1, S2, S3 и т. д. Если в результате величина P дает превышение над «фоном», а еще лучше – над каждым «локальным» оптимумом, микробиологи считают, что нашли оптимальное соотношение компонентов в среде.
Однако для такого заключения не всегда достаточно оснований. Если, например, выход процесса соответствует рассмотренному семейству характеристик, то из него при величине фактора S1 = (S1)1 варьируя фактор S2 на всех 5 уровнях, можно заключить, что оптимальное значение фактора S2 находится где-то в диапазоне между S2 = (S2)2...(S2)3. Посмотрев же на семейство характеристик в целом (т.е. проведя тотальный перебор), можно убедиться, что оптимальное значение фактора S2 равно или даже больше (S2)4, а фактора S1 – где-то между (S1)3 и (S1)4. Это показывает ненадежность выводов в методе отдельного изучения каждого фактора.
Отсюда следует также, что такой метод будет вполне приемлем при симметричном виде зависимости P(S1, S2,…,Sn), а это совсем не обязательно имеет место.
Метод Гаусса – Зайделя. Микробиологи называют этот метод «последовательным изучением каждого фактора». Здесь частные зависимости P (S1), P (S2), P (Sn) находят не сразу на одном и том же «фоне», а по очереди. Сначала определяют P (S1), анализируют эту зависимость, находят частный оптимум для фактора S1, затем меняют «фон», установив в нем значение S1, равное этому частному оптимуму.
Далее на новом «фоне» изучают влияние фактора S2, отыскивают его частный оптимум, снова меняют «фон», добавив в него новое значение S2, и так продолжают с факторами S3, S4,…,Sn, каждый раз (т. е. после каждой серии экспериментов) изменяя «фон».
Закончив изучение последнего фактора, считают задачу выполненной и объявляют «оптимальное» соотношение уровней факторов. И опять не совсем правильно. Ведь вполне могло быть, что на старом «фоне» частный оптимум для фактора S1 или S2 мог отличаться от общего оптимума (что мы и видим в том же примере, приведенном на семействе характеристик). Поэтому, строго говоря, метод Гаусса – Зайделя следует повторять и дальше (перейдя к новому циклу изучения факторов), пока частные оптимумы по отдельным факторам не перестанут изменяться от одной серии опытов к другой.
Этот метод имеет и еще один недостаток по сравнению с предыдущими: необходимо поочередное выполнение серий экспериментов, так как изменение «фона» требует анализа результатов каждой серии. Между тем при проведении экспериментов в колбах можно единовременно ставить большую серию экспериментов с различным составом среды в разных колбах, и это удобно, так как длительность эксперимента может быть очень велика.
Представим теперь графически метод Гаусса – Зайделя на топографической карте «поверхности отклика» для двух факторов (рис. 7.4).
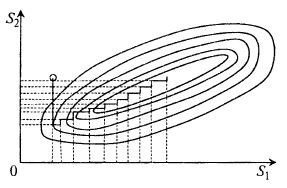
Рис. 7.4. Процедура оптимизации по методу Гаусса–Зайделя
Из рисунка видно, что для поверхностей отклика типа «хребтов» движение к оптимуму методом Гаусса – Зайделя идет весьма медленно.
Чем больше количество факторов, тем более длителен путь движения к оптимуму и тем больше вероятность ошибки в определении оптимума при отказе от продолжения варьирования факторов.

