Расчет программы крутого восхождения. После скучных, но необходимых расчетов значимости коэффициентов и адекватности уравнения в целом вернемся к главной задаче – расчету программы крутого восхождения.

Для данного примера рассчитываем условия для 6 шагов крутого восхождения, т. е. 6 новых сред.

На каждом шаге к предыдущему уровню фактора (начиная от исходного уровня – центра планирования) прибавляется или от него отнимается рассчитанное значение шага. По наиболее критичному фактору последний шаг будет совпадать с максимальным или минимальным его уровнем, по другим факторам – несколько не доходить до них. Теперь можно составлять 6 сред крутого восхождения и воспроизводить процесс с этими рассчитанными средами. Здесь важно не забыть, что для факторов с отрицательным значением коэффициента регрессии при каждом шаге отнимается, а не прибавляется величина рассчитанного ΔS_i.

Анализ результатов крутого восхождения. На основании намеченной программы крутого восхождения можно рассчитать ожидаемые результаты выхода при сохранении адекватности описывающего уравнения. Для этого сначала нужно все значения уровней факторов пересчитать в кодированные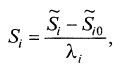
(7.15)
а затем рассчитать величину Pˆ аналогично тому, как это делалось для опытов в исследовательской матрице, подставив вместо кодированных значений S_i (–1) и (+1) значения, вычисленные по формуле Х7.15). Например, для опыта 11 ожидаемое (расчетное) значение Pˆ составит: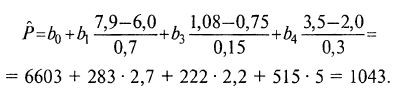

В специальном столбце табл. 7.4 приведены результаты расчетных значений выхода в программе Kpyioro восхождения.

Далее следует поставить опыты с рассчитанными значениями факторов.

В колонке рядом с расчетными данными приведены экспериментальные. Очевидно, что столь высоких значений выхода, как ожидали, мы не получаем. Более того, рост выходного показателя идет не все время – после 4-го шага (12-го опыта ) начинается даже падение выхода. Но это не должно смущать. Мы ведь и не рассчитывали на то, что уравнение идеально описывает всю область варьирования факторов. Вполне возможно, что линейное приближение недостаточно. Но направление движения к оптимуму найдено. Более того, за один проход результат увеличен с 6603 (среднее по матрице планирования) до 8510. Далее нужно поставить новую матрицу планирования с центром в новой точке и наметить программу крутого восхождения.

Обычно уже за один цикл исследовательской матрицы и крутого восхождения получается довольно заметное увеличение выхода. Но в принципе расчет по этому методу необходимо повторять до тех пор, пока линейное уравнение не станет неадекватным. В этом случае надо использовать другие методы, описывающие процесс уже уравнением второго порядка:
(7.16)

Здесь кроме линейных членов b_iS_i появляются еще и квадратичные b_iiS_i², а самое главное – еще и так называемые «коэффициенты взаимодействия», которые учитывают взаимовлияние факторов.

Для таких уравнений существуют и специальные планы эксперимента, и специальные методы оптимизации.