Наиболее распространены уравнения, описывающие кинетику в зависимости от концентрации лишь одного субстрата, который называют лимитирующим; другие субстраты при этом полагаются находящимися в избытке и не влияющими на скорость роста.

Мы уже рассматривали одну модель, она вытекает из самого определения удельной скорости роста μ:
 (8.1)

Неявно предполагается, что величина μ здесь постоянна, однако это не так – она строго зависит от концентрации субстрата. Задача как раз в том и состоит, чтобы найти эту зависимость.

В зависимости от штамма и вида микроорганизма, а также и субстрата связь µ(S) может иметь самый различный характер.

Далее рассмотрим варианты этой связи.

Модель Кобозева. Эта простейшая модель дает аналогию с химической кинетикой:
 (8.2)
(где К – константа скорости), или
µ= KS      (8.3)

Графически эта модель представлена на рис. 8.2. Модель Блэкмана при малых концентрациях дает то же уравнение, однако при достижении величиной S некоторого критического уровня S* скорость роста прекращает увеличиваться: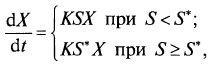
 (8.4)
или
 (8.5)

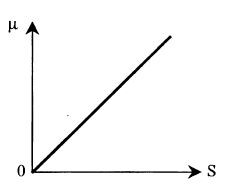
Рис. 8.2. Зависимость удельной скорости роста микроорганизмов от концентрации субстрата, подчиняющаяся химической кинетике (модель Кобозева)

Графически модель Блэкмана представлена на рис. 8.3.

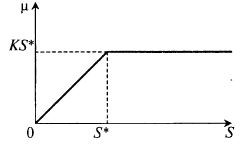
Рис. 8.3. Зависимость удельной скорости роста микроорганизмов от концентрации субстрата по модели Блэкмана

Модель Моно. Эта модель основана на ферментативной кинетике протекающих в клетках биохимичес- ких превращений и наиболее широко известна: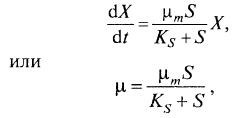
 (8.6)
где µ_m и K_s – константы.

Характерные точки для графика μ(S), представленного на рис. 8.4, легко найти простой подстановкой в уравнение (8.7) значений S:

μ = 0 при S = 0;      (8.8)

μ = μ_m при S → ∞;      (8.9)

μ = μ_m/2 при 5 = K_s.     (8.10)

Величину K_s и μ_m проще определить, используя график в обратных координатах (метод Лайнуивера и Бэрка):
 (8.11)

Этот график приведен на рис. 8.5,а.

Из уравнения (8.11) можно получить:
    (8.12)                      (8.13)

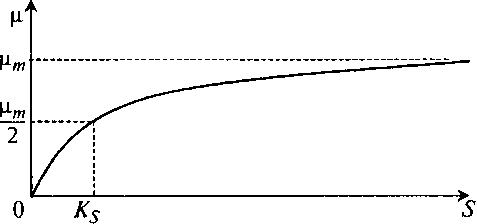
Рис. 8.4. Зависимость удельной скорости роста
от концентрации субстрата по модели Моно

Из рис. 8.5,а видно, как можно получить значения \/\хт и 1 /Ks, построив прямую по экспериментальным точкам.

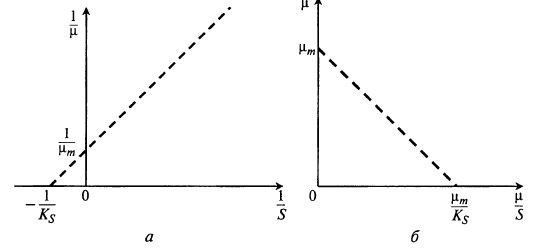
Рис. 8.5. Нахождение параметров уравнения Моно методом Лайнуивера и Бэрка (а)
и методом Корниш-Боудена (б)

Есть еще один метод определения µ_m и K_s (метод Корниш- Боудена).

Умножив уравнение (8.11) на μμ_m, найдем:
     (8.14)

Отсюда графически получаем прямую в координатах μ – μ/S. Из уравнения (8.14) определим:
    (8.15)                    (8.16)

Расположив экспериментальные точки на этом графике, легко на осях координат найти искомые величины (рис. 8.5, б).

Модель Мозера учитывает сигмоидальный характер зависимости μ(S), представленной на рис. 8.6:
(8.17)
Здесь К – новый по сравнению с уравнением Моно параметр, причем К > 1.

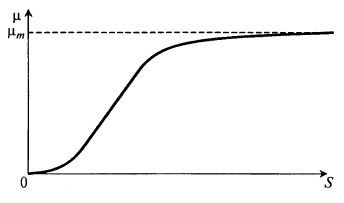
Рис. 8.6. Зависимость μ(S) по уравнению Мозера

Как и в уравнении Моно,

при S = 0 μ = 0;     (8.18)

при S → ∞ μ → μ_m,      (8.19)

но
 (8.20)

Модель Перта учитывает зависимость μ(S) не для лимитирующего, а для «стимулирующего» субстрата (рис. 8.7) и описывается уравнением
   (8.21)

Из уравнения (8.21) следует, что при S = 0 μ = μ₀, т. е. μ ≠ 0.

Это значит, что даже при отсутствии данного субстрата уже есть некоторый рост микроорганизмов. Видимо, в среде есть некий другой субстрат. Дальнейшее увеличение удельной скорости роста описывается вторым членом уравнения (8.21), который похож на уравнение Моно, где вместо µ_m стоит новый параметр μ_i. Из уравнения получается, чтопри S → ∞ μ → (μ₀ + μ₁, как и показано на рис. 8.7.

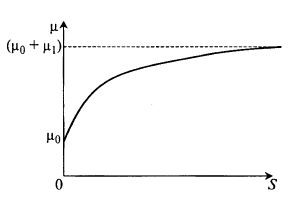
Рис. 8.7. Зависимость μ(S) по уравнению Перта

Модель Андрюса учитывает ингибирование повышенными концентрациями субстрата (рис. 8.8) и описывается уравнением
     (8.22)

Это уравнение отличается от уравнения Моно наличием в знаменателе квадратичного члена S² с новым кинетическим параметром K_i.

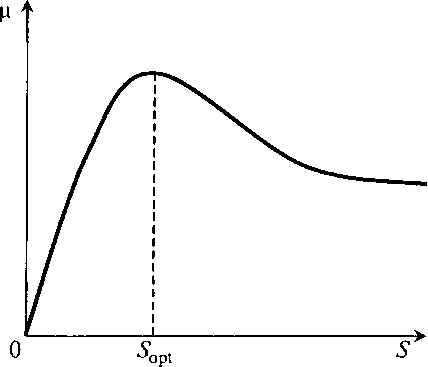
Рис. 8.8. Зависимость μ(S) с ингибированием повышенными
концентрациями субстрата по модели Андрюса

Из рис. 8.8 видно, что зависимость μ(S) γιο Андрюсу имеет явный экстремум.

Можно определить, при какой величине S значение μ будет максимальным. Для этого

найдем производную по S и приравняем ее нулю: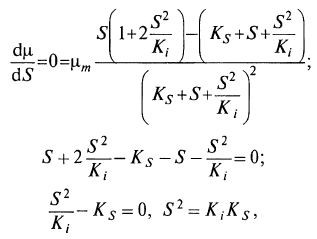
 (8.23)
откуда оптимальное значение концентрации субстрата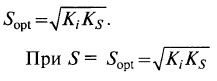
 (8.24)  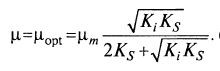                           (8.25)

Выражение (8.25) можно свести к следующему: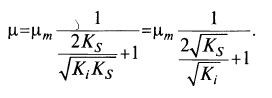
 (8·26)

Отсюда следует, что μ даже в точке экстремума меньше μ_m.

Заканчивая изложение субстрат-зависимых моделей удельной скорости роста микроорганизма, можно построить сравнительный график (рис. 8.9), показывающий характерные особенности всех рассмотренных моделей, их сходство и отличия.

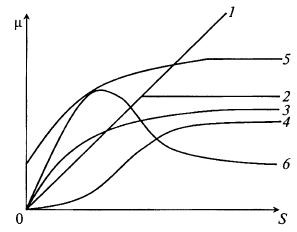
Рис. 8.9. Сравнительный график зависимостей удельной скорости роста
микроорганизмов от концентрации субстрата по уравнениям:
1 – Кобозева; 2 – Блэкмана; 3 – Моно; 4 – Мозера; 5 – Перта; 6 – Андрюса