Рост микроорганизмов зависит не только от концентрации субстрата S, но также и от концентрации продуктов метаболизма P. Причем чаще всего накопление продуктов снижает (ингибирует) скорость роста. Это ингибирование учитывается различными моделями.
Модель Хиншельвуда. Наиболее простым является уравнение, предложенное Хиншельвудом:
μ = μm-ΚΡ. (8.27)
Графическое выражение этого уравнения дано на рис. 8.10.
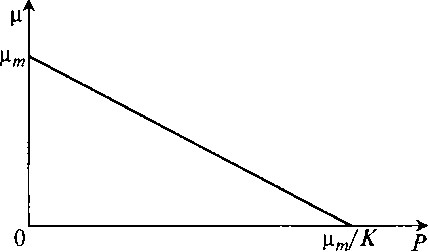
Рис. 8.10. Ингибирование роста микроорганизмов продуктом метаболизма по модели Хиншельвуда
В уравнении (8.27) при P = 0 μ = μm, при μ = 0 P = μm/K, что позволяет легко определять кинетические параметры μm и К.
Модель Иерусалимского. Модель Иерусалимского, подобно модели Моно, базируется на ферментативной кинетике и описывается уравнением
(8.28)
или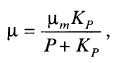
где Kp – константа ингибирования; μm – максимальная удельная скорость роста.
Графическое выражение зависимости дано на рис. 8.11.
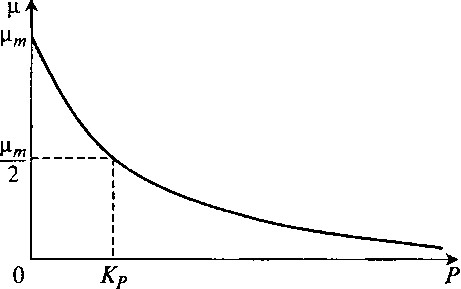
Рис. 8.11. Зависимость μ(Ρ) по модели Иерусалимского
Характерные точки зависимости можно получить подстановкой разных значений P в уравнение (8.28):
при P = 0 μ = μm; (8.30)
при Р → ∞ μ → 0; (8.31)
при P = Kp μ = 0,5 μ. (8.32)
Уравнение (8.28) можно преобразовать в координаты Лайнуивера и Бэрка:
(8.33)
В этом уравнении
при 1/μ = 0 P = –КР; (8.34)
при P = 0 1/μ = 1/μ (8.35)
Само уравнение (8.33) в координатах P – 1/μ выгладит как прямая (рис. 8.12).
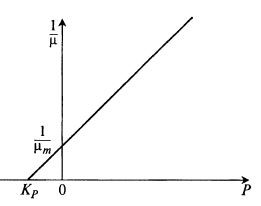
Рис. 8.12. Определение кинетических параметров μm и Kp уравнения Иерусалимского
Модель Бергтера. Уравнение Бергтера учитывает сигмоидаль- ный характер зависимости μ(Ρ), отражающей ингибирование роста микроорганизмов продуктом метаболизма (рис. 8.13):
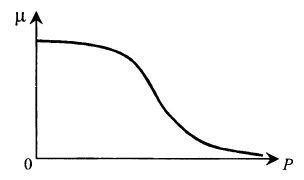
Рис. 8.13. Зависимость μ(Ρ) по модели Бергтера
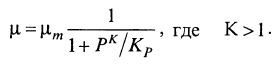
Частично ингибирующий продукт. Бывают ситуации, когда продукт как бы частично инги- бирует скорость роста микроорганизмов (не до нуля). Эта ситуация графически выражена на рис.8.14 и может быть описана уравнением, подобным уравнению Перта для стимулирующего субстрата (8.21):
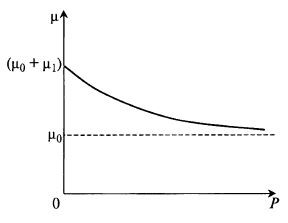
Рис. 8.14. Влияние частично ингибирующего продукта на удельную скорость роста микроорганизмов
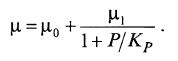
Стимулирующий продукт. Изредка встречается процесс, в котором выделяемый клетками
продукт метаболизма не ингибирует, а стимулирует рост культуры. Эта ситуация отражена на рис. 8.15 и может быть описана уравнением Перта (8.21) для стимулирующего субстрата, каковым, по существу, и является такой продукт: (8.38)
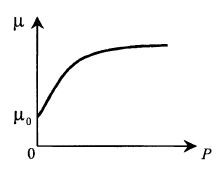
Рис. 8.15. Влияние стимулирующего рост продукта метаболизма на удельную скорость роста микроорганизмов
Аналогично тому, как это сделано для различных субстратов, интересно провести сравнение влияния продуктов метаболизма на рост микроорганизмов по различным моделям. Такое сравнение представлено на рис. 8.16.
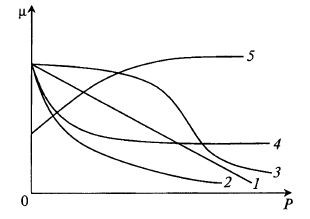
Рис. 8.16. Сравнительный график различных моделей влияния продуктов метаболизма на рост микроорганизмов:
1 – модель Хиншельвуда; 2 – модель Иерусалимского; 3 – модель Бергтера; 4 – частично ингибирующий продукт; 5 – стимулирующий продукт
В разделах 8.1 и 8.2 мы рассматривали однофакторные зависимости пока только для двух типов влияния факторов – субстрата и продукта. Не забудем, что к субстратам можно отнести растворенный кислород (в аэробных процессах), а к продуктам – растворенный диоксид углерода.
Возникает вопрос: как влияет сама биомасса микроорганизмов? Прежде всего общая скорость роста обычно тем больше, чем выше концентрация биомассы X. А удельная скорость μ? Здесь концентрация биомассы косвенно представляет собой концентрацию неизмеряемого продукта метаболизма, который может ингибировать рост. И зависимости при этом похожи, только вместо P подставляют в уравнения величину X.
П. И. Николаевым было предложено для учета влияния ингибирующего продукта метаболизма заменять концентрацию неизмеряемого продукта на комплекс (S0-S). Это относится к тем процессам, где продукт метаболизма выделяется пропорционально потребленному субстрату.

