Мы рассмотрели варианты различных уравнений роста биомассы (и ее деградации) и биосинтеза продукта (и его инактивации).

Чтобы «замкнуть» материальный баланс, в котором почти во всех уравнениях участвует концентрация субстрата, необходимо дополнить его уравнением кинетики потребления субстрата.

Это уравнение в общем виде может быть представлено как аддитивное, в правой части которого фигурируют затраты на собственно рост микроорганизмов (Q₁), на образование продукта метаболизма (Q₂) и на поддержание жизнедеятельности (Q₃):
 (8.98)

Два первых члена уравнения связаны с соответствующими скоростями роста биомассы Q_X и продукта метаболизма Q_P выходными коэффициентами Y_XS и Υ_PS·
Q₁ = Q_X/Y_XS, (8.99) Q₂ = Q_P/Y_PS (8.100)

Особо следует сказать о затратах субстрата на поддержание жизнедеятельности.

В клетках микроорганизмов все время идут процессы деградации (разрушения) некоторых веществ (белков, нуклеиновых кислот и др.) и одновременно – процессы их синтеза. Вместе взятые эти два процесса можно назвать процессом «репарации», т.е. регенерации утраченных веществ. На этот процесс необходимо расходовать часть субстрата.

Кроме того, субстрат расходуется на синтез определенных, тоже неизмеряемых продуктов метаболизма, образующихся в небольшом количестве.

Особенно это заметно в том случае, когда в конце процесса субстрат исчерпан, рост биомассы и образование целевого продукта прекратились. Если при этом подавать субстрат с небольшой скоростью, то можно создать условия, при которых концентрации биомассы и продукта не возрастали и не падали бы, а сохранялись на постоянном уровне. В этом случае субстрат все время добавляется (т. е. ΔS ≠ 0), а биомасса и продукт метаболизма не меняются (т.е. ΔX = 0 и ΔΡ= 0). Благодаря подаче субстрата не наступает фаза отмирания клеток микроорганизмов.

Это дополнительное расходование субстрата происходит не только в конце ферментации, а в течение всего процесса. Просто эти расходы субстрата обычно «приписывают» к расходам на рост (Q₁) и на образование продукта метаболизма (Q₂).

Правильно было бы выделить эту статью расхода в отдельный член уравнения – на поддержание жизнедеятельности микроорганизмов Q₃.

Вполне очевидно, что эта величина пропорциональна концентрации микроорганизмов:
Q₃ = m_S X, (8.101)

где m_S – коэффициент поддержания жизнедеятельности, или удельная скорость расходования субстрата на поддержание жизнедеятельности микроорганизмов.

С учетом соотношений (8.99) – (8.101) уравнение (8.98) можно записать следующим образом: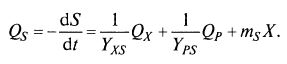
 (8.102)

В этом уравнении коэффициенты Y_XS и Y_PS отличаются от экономических коэффициентов, рассмотренных в главе 4. Математическая модель (8.102) более правильно учитывает различные пути расходования субстрата. В экономических коэффициентах мы не выделяли «невидимой» части субстрата, расходуемой на поддержание жизнедеятельности. Поэтому полученные «экономические» коэффициенты приписывали весь расход субстрата чему-то одному – образованию биомассы или продукта метаболизма.

Так, например, если за период времени Δt образовалось ΔX биомассы и ΔP продукта и при этом израсходовалось ΔS субстрата, мы вычисляли экономические коэффициенты по биомассе и продукту таким образом:

Этот способ вычисления неправилен, так как образуется и то, и другое, да еще существуют затраты субстрата на поддержание жизнедеятельности.

Как правильно определять эти коэффициенты?

Необходимо находить их все сразу по уравнению
 (8.103)

Для каждого интервала времени Δt можно определить ΔX, ΔP и X (берут среднее значение для интервала). Подставив найденные числовые значения, получаем линейное уравнение со следующими тремя неизвестными: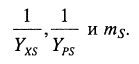

Ясно, что одного интервала для определения всех трех коэффициентов недостаточно. Нужны как минимум 3 точки, которые дадут 3 уравнения, из них можно найти все 3 коэффициента.

Лучше взять больше точек, чем число искомых коэффициентов, тогда получится система уравнений (столько же, сколько взято измеренных точек – интервалов ферментации), в которой коэффициенты находят методом наименьших квадратов.

Иногда можно и упростить решение. Например, в стационарном режиме ΔХ/Δt = 0 получается 2 уравнения с 2 неизвестными – их проще решить.

Или можно найти период времени, где не было ни роста биомассы, ни образования нового продукта.

В качестве примера решения можно рассмотреть данные табл. 8.2.

Таблица 8.2. Расчет коэффициентов выхода Yxs и Yps и скоростей роста
и биосинтеза продукта по данным периодической ферментации

На основании данных таблицы можно записать уравнения материального баланса (для каждого из 3 интервалов):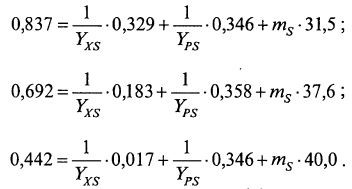

Решение системы уравнений дает коэффициенты:
Y_XS = 1,82; Y_PS = 0,36; m_S =0,011.

Следует отметить, что эти коэффициенты уже не будут меняться в ходе процесса так сильно, как упомянутые ранее экономические.

Показатель ms по смыслу является кинетическим и может по- разному зависеть от других показателей процесса.

Для неэнергетических субстратов, таких, как азот, макро- и микроэлементы,
m_S = 0. (8.104)

Показатель ms не изменяется в процессе ферментации:
m_S = + m. (8.105)

Экзотический случай, когда субстрат при ферментации дополнительно образуется в процессе поддержания жизнедеятельности микроорганизмов:
m_S = –m. (8.106)

Чем больше концентрация субстрата, тем больше его расходы на поддержание жизнедеятельности микроорганизмов:
m_S = KS. (8.107)

Расходование субстрата в «побочных» биохимических процессах происходит по ферментативной кинетике Михаэлиса–-Ментен:
 (8.108)

Субстрат более интенсивно расходуется на поддержание жизнедеятельности микроорганизмов при его пониженных концентрациях:
 (8.109)

Продукт метаболизма стимулирует расходование субстрата на поддержание жизнедеятельности микроорганизмов:
 (8.110)

Существует графический метод определения коэффициентов Y_XS и m_S по экспериментальным данным. Этот метод вытекает из уравнения
 (8.111)

Если представить экспериментальные данные в системе обратных координат (1l/Y*_XS, 1/μ), то получим прямую (рис. 8.34).

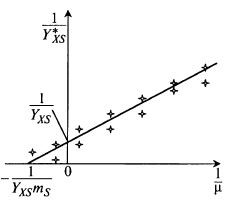
Рис. 8.34. Графическое представление выходных коэффициентов
в системе обратных координат (1/Y*_XS, 1/μ)

Эта прямая отсекает на оси ординат отрезок 1/Y*_XS = 1/Y_XS, а на оси абсцисс – отрезок 1/μ = – 1 /(m_S/Y_XS), откуда легко найти m_S.

Или если выразить данные в координатах (qs, μ), где qs =––, то их можно также аппроксимировать прямой (рис. 8.35):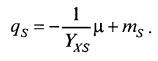 
 (8.112)

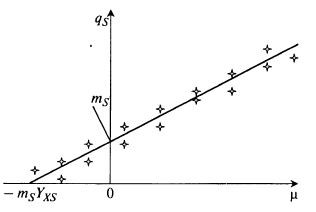
Рис. 8.35. Определение коэффициентов m_S и Y_XS графическим методом в координатах (q_S, μ)

Она отсекает на оси ординат отрезок, равный m_S, а на оси абсцисс – отрезок μ = – m_SY_XS, откуда можно найти Y_XS.

Для неэнергетических субстратов (минеральный азот, микро- и макроэлементы, фосфор) обычно затраты на поддержание жизнедеятельности нулевые, в связи с чем упрощаются расчеты материальных балансов.