Поскольку периодический и полупериодический процессы являются нестационарными (в них все параметры изменяются во времени), логично ожидать, что и значения режимных параметров должны изменяться во времени, а не быть постоянными, как в непрерывных процессах.

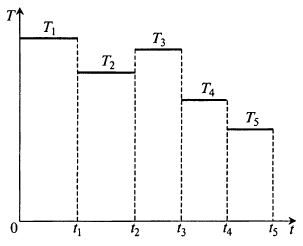
Подбор переменных во времени профилей параметров трудно проводить методами статистического планирования эксперимента (хотя и возможно). В этом случае каждый параметр распадается как бы на несколько отдельных параметров, характеризующих его значение в определенный период ферментации (для температуры эта ситуация представлена на рис. 10.1).

Рис. 10.1. Представление профиля изменения температуры во времени
как совокупности постоянных значений температуры для различных
участков ферментации:
T₁, Т₂, T₃, 7₄, T₅ – значения температур для временных диапазонов
O-t₁, t₁ – t₂, t₂ – t₃, t₃ – t₄, t₄ – t₅ соответственно

Число оптимизируемых факторов при этом резко возрастает, возрастает и число опытов, необходимых для экспериментального отыскания нужного профиля.

Кинетические модели дают больше возможностей для определения оптимальных профилей изменения режимных параметров во времени.

Конкретизируем задачу оптимизации. Речь пойдет о процессах, в которых целевым продуктом является не биомасса, а продукт метаболизма. Критерием оптимальности таких процессов для простоты будем считать концентрацию продуктов метаболизма в конце ферментации (хотя возможны и другие критерии, которые мы рассматривали при оптимизации ферментационных сред).

Рассмотрим простейшую задачу оптимизации периодического процесса по одному режимному параметру (т. е. регулируемому в ходе всего процесса), например по температуре Т.

Запишем простейшую систему кинетических уравнений:

 (10.1)           (10.2)
P → шах при t = t_K (время цикла ферментации). (10.2)

Зависимость μ и q_P от температуры представим на одном графике. Пока не будем расшифровывать аналитический вид этих зависимостей.

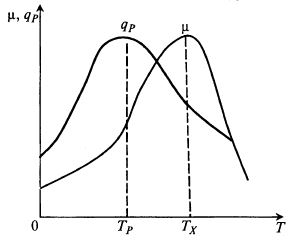
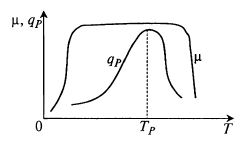
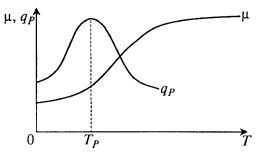
В общем случае зависимости μ(T) и q_P(T) имеют экстремальный характер, а значения температуры, оптимальные для роста микроорганизмов и для биосинтеза продукта, не совпадают (рис. 10.2). Температуру, оптимальную для удельной скорости роста биомассы, обозначим T_X, а оптимальную для биосинтеза для удельной скорости биосинтеза продукта – Т_Р. Возможны и другие варианты. Например, одна из зависимостей может представлять собой плато, охватывающее оптимум на второй (рис. 10.3), или одностороннее плато, выходящее за пределы оптимума второй зависимости (рис. 10.4), или, наконец, оптимумы зависимостей могут совпадать, т. е. T_X= T_P (рис. 10.5).

Рис. 10.2. Взаимное положение кинетических
зависимостей роста (μ) и биосинтеза (q_P)
от температуры при несовпадающих оптимумах

Рис. 10.3. Взаимное положение кинетических
зависимостей при широком плато оптимума
по росту (μ) и остром оптимуме по биосинтезу
продукта (q_P), охватываемом диапазоном оптимального роста

Рис. 10.4. Взаимное положение кинетических
зависимостей при широком плато оптимума
по росту (μ) и остром оптимуме по биосинтезу
продукта (q_P) в зоне температур, не оптимальных
для роста микроорганизмов

Рис. 10.5. Взаимное положение кинетических
зависимостей с совпадающими положениями
оптимума по росту микроорганизмов (μ)
и биосинтезу продукта (q_P)

Это соотношение оптимумов зависимостей μ и q_P от величины фактора является важным свойством процесса ферментации, в конечном счете определяющим характер режима управления процессом.

Конкордантными называются факторы, для которых положение оптимума биосинтеза продукта метаболизма находится в зоне, оптимальной и для роста биомассы микроорганизмов (рис. 10.3 и 10.5).

Дискордантными называются факторы, для которых оптимум по биосинтезу продуктов метаболизма не совпадает с оптимумом для роста микроорганизмов, т. е. T_X ≠ T_P (рис. 10.2 и 10.4).

Приведенные определения относятся не только к температуре, но и к любым другим факторам (технологическим параметрам), влияющим на рост биомассы микроорганизмов и биосинтез продукта метаболизма.

Хотя система уравнений (10.1) – (10.3) кажется простой, ее решение, как правило, возможно не аналитически, а с применением компьютерных программ.

Здесь сразу можно отметить особый частный случай для конкордантных факторов. Профиль во времени конкордантного режимного параметра (фактора) вырождается в величину постоянную. Температура, являющаяся оптимальной как для роста, так и для биосинтеза продукта, должна поддерживаться в течение всего периода ферментации.

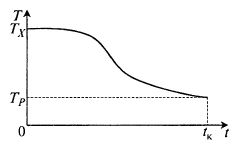
Более сложная ситуация возникает при несовпадающих оптимумах (для дискордантных факторов). В этом случае, как правило, необходимо иметь переменный во времени профиль температуры, изменяющийся от величины T_X, оптимальной для роста микроорганизмов, до величины T_P, оптимальной для биосинтеза продукта (рис. 10.6). Расчет этого профиля довольно сложен.

Рис. 10.6. Примерный вид оптимального профиля
при управлении по дискордантному фактору