Для описания кинетики этих сложных химических превращений примем, что каждая из входящих в систему реакций является простой химической реакцией, описываемой уравнением кинетики, в котором скорость протекания реакции пропорциональна произведению концентраций реагирующих веществ на соответствующую константу скорости реакции.

Из структуры уравнений видно, что фермент-субстратный комплекс EС может образовываться и вновь распадаться, т. е. это процесс обратимый. Обозначим константу скорости прямой реакции K₁ а обратной – K_–1 константу скорости образования продукта из фермент-субстратного комплекса обозначим K₂:
 (12.3)

Запишем материальный баланс для образования фермент-субстратного комплекса (ES)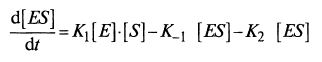
 (12.4)
и материальный баланс для образования продукта P
 (12.5)

Особенность ферментативной кинетики состоит в том, что реакции образования и распада комплекса ES протекают гораздо быстрее, чем процесс образования конечного продукта реакции Р.

В связи с этим концентрация комплекса [ES] быстро устанавливается на некотором постоянном уровне, а сама реакция имеет стационарный характер по [ES], или квазистационарную кинетику.

Иначе говоря, можно принять
 (12.6)

Отсюда можем получить выражение для [jES]: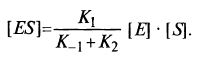
 (12.7)

Интересно отметить, что фермент в процессе реакции не расходуется. Его начальная концентрация [E]₀ просто раскладывается на свободный фермент и фермент-субстратный комплекс:
[Е]₀=[Е] + [ES]. (12.8)

Если подставить сюда выражение для [ES], то можно получить зависимость для концентрации свободного фермента [E]: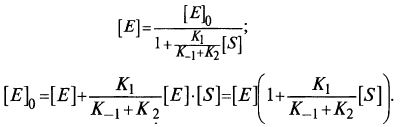
 (12.9)

Подставим теперь это выражение в формулу (12.7) для концентрации фермент-субстратного комплекса [ЕS]: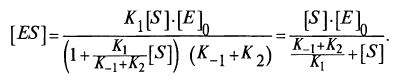
 (12.10)

Найдем окончательное выражение для скорости образования продукта реакции: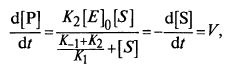
 (12.11)
где V – скорость ферментативной реакции.

Это уравнение, предложенное в начале XX в. двумя авторами – Михаэлисом и Ментен (женщина-ученый), называют уравнением Михаэлиса–Ментен. Если ввести обозначение
K_M = (K_–1 + K₂)/K₁ (12.12)
где K_M – константа Михаэлиса, и опустить квадратные скобки в обозначении концентраций Е, S и Р, то уравнение (12.11) преобразуется к виду
 (12.13)

Обратите внимание на сходство этого уравнения с уравнением Моно. Здесь dP/dt или V подобно Q_X или dX/dt; E₀ подобно концентрации биомассы в уравнении Моно, а константа Михаэлиса Ku аналогична субстратной константе Моно K_S.

Это сходство не случайно. Именно имея в виду ферментативный характер превращений субстрата микроорганизмами, Моно предложил форму уравнения, подобную уравнению Михаэлиса–Ментен.

Как определить количество фермента в исходной среде E₀ или в системе после протекания реакции?

Для всех других участников ферментативной реакции – субстрата или продукта – существуют количественные методы, позволяющие точно определить массу вещества.

Для ферментов же часто даже неизвестна молекулярная масса – она обычно весьма велика, а ферменты представляют собой не чистое вещество, а смесь с белками и другими ферментами.

Фермент «взвешивают» не в граммах, а в единицах активности.

Единица активности – это такое количество фермента, которое при 30 °C за 1 минуту превращает 1 микромоль субстрата в продукт. Скорость реакции зависит еще и от концентрации субстрата и величины рН. Для каждого фермента эти стандартные условия его «взвешивания» заранее определены. Таким образом, количество фермента определяется по кинетике модельной реакции, и точное определение приходящейся на единицу активности массы фермента обычно неизвестно. Можно лишь определить концентрацию фермента в единице массы или объема вещества, проявляющего ферментную активность, но в ед/г или ед/мл (здесь «ед» – единица активности фермента).

В уравнении Михаэлиса–Ментен произведение K₂E₀ можно заменить на V_max, а скорость образования продукта обозначить через V.

В результате получается принятый в ферментативной кинетике вид уравнения:
 (12.14)

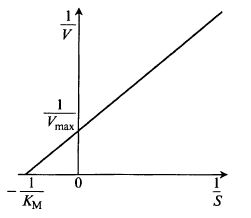
Как и в любом кинетическом уравнении, возникает проблема определения констант V_max и К_M по экспериментальным данным. Для этого, аналогично уравнению Моно, используют координаты Лайнуивера и Бэрка (рис. 12.2):

 (12.15),   (12.16),   (12.17)

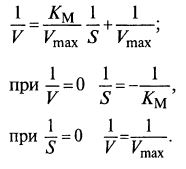
Рис. 12.2. Определение коэффициентов уравнения
методом Лайнуивера и Бэрка (двойных обратных координат)

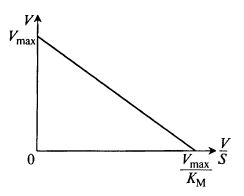
Другой вариант – координаты Корниш-Боудэна (V и V/S):

 (12.18),   (12.19),   (12.20)

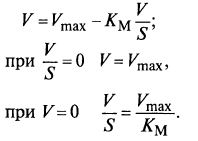
На рис. 12.3 показано, как выглядит уравнение (12.8) в этих координатах.

Рис. 12.3. Определение коэффициентов
уравнения методом Корниш-Боудэна

Все эти способы были предложены специалистами по ферментативной кинетике.