В любом микробиологическом процессе ключевую роль играет культура используемых микроорганизмов. В промышленной мик­робиологии широко применяются плесневые грибы, дрожжи, актиномицеты, бактерии и водоросли в виде чистых или сме­шанных культур. В традиционных процессах ферментации пред­почтение обычно отдается смешанным культурам, а в большин­стве современных ферментационных процессов — монокультурам, выращиваемым в асептических условиях. Говорить об идеаль­ных культурах можно лишь в самых общих чертах. Следует отдавать себе отчет в том, что идеального микроорганизма не существует, а разнообразие продуктов, которые можно получать с помощью микроорганизмов, определяется разнообразием са­мих микроорганизмов и их субстратов. Впрочем, возможно, ког­да-нибудь мы и сумеем создавать такие идеальные микроорга­низмы с помощью генетической инженерии и тем самым опро­вергнем высказанное выше утверждение. Большинство исполь­зуемых сегодня культур получено из природных источников; однако эти культуры были затем улучшены или путем выращи­вания в условиях, характерных для данного процесса (для по­вышения выхода биомассы и первичных метаболитов), или с по­мощью мутагенеза (для производства вторичных метаболитов).

Приведем основные уравнения, описывающие рост микроор­ганизмов, в частности одноклеточных, в ферментерах и в других микробиологических реакторах. Для выращивания любой куль­туры необходимы: 1) жизнеспособный посевной материал; 2) источники энергии и углерода; 3) питательные вещества для синтеза биомассы; 4) отсутствие ингибиторов роста; 5) соответ­ствующие физико-химические условия.

Если все эти требования выполнены, то скорость роста (уве­личения биомассы) одноклеточных микроорганизмов с бинар­ным делением, размножающихся в условиях хорошо перемеши­ваемой периодической культуры, будет пропорциональна кон­центрации микробной биомассы, т. е.

  где dx/dt- скорость роста, μ-коэффициент пропорционально­сти, обычно называемый удельной скоростью роста, х— концент­рация биомассы (на сухой вес).      Если μ— постоянная величина, уравнение (1) можно преобразовать и проинтегрировать:

 (2)

где Xo — концентрация микробной биомассы в момент времени /=0, t — время. Уравнение (2) можно переписать в виде:

  (3) , откуда  (4)

Если построить график зависимости Inx от времени, то мы по­лучим прямую с наклоном μ. Такой рост называют экспонен­циальным или логарифмическим; он имеет место тогда, когда состав микробной биомассы и условия окружающей среды оста­ются постоянными. Приведенные выше уравнения применимы и к смешанным культурам, в которых одноклеточные организмы равномерно распределены в культуральной среде.

 При описании роста микроорганизмов с бинарным делением в периодических культурах широко используется величина, ха­рактеризующая время удвоения биомассы. Связь между удель­ной скоростью роста μ и временем удвоения биомассы t_y можно 'найти из уравнения (3), заменив х на 2x₀, a t — на t_y:  

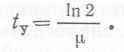 (5)

• 10.2.1. Эффективность роста: коэффициент выхода биомассы

При любой количественной оценке роста микроорганизмов и/или синтеза конечного продукта необходимо связать образование микробной биомассы и продуктов с расходованием субстратов и питательных веществ. Для описания соотношения между ро­стом микроорганизмов (в расчете на сухой вес) и потреблением углеродного энергетического субстрата были введены понятия урожая бактериальной культуры и выхода биомассы (AIonocK 1942). В математической форме коэффициент выхода микроб­ной биомассы Yχ∕_s можно представить следующим образом:

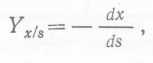(6)

где ds — бесконечно малое уменьшение концентрации субстрата^ соответствующее бесконечно малому увеличению концентрации микробной биомассы dx. Знак минус указывает, что знаки из­менения XHS противоположны. При постоянных условиях роста коэффициент выхода остается постоянным, т. е. если Xo и So — 'Концентрации субстрата и биомассы в момент времени to, а х и s — в момент I, то:

 (7)

В общем случае коэффициент выхода биомассы является пере­менной величиной, зависящей от условий культивирования. Ва­риабельность этого коэффициента очень важна с точки зрения оптимизации процесса. Понятие коэффициента выхода можно распространить на все разнообразие питательных веществ, ис­пользуемых растущими микроорганизмами, и на все получаю­щиеся продукты. Кроме того, при оценке относительной эффек­тивности биохимических путей, лежащих в основе роста и ме­таболизма микроорганизмов, широко применяют понятия мо­лярного урожая биомассы и выхода, когда учитывается число электронов, поступающих от субстратов, и суммарное количе­ство потребляемой энергии.

Когда микроорганизмы растут на хорошо растворимых суб­стратах, коэффициент выхода и коэффициент конверсии совпадают; однако при росте на плохо растворимых и несмешиваю- щихся субстратах они могут заметно различаться. Коэффициент конверсии можно определить как количество микробной био­массы, образующейся на единицу массы субстрата.

Для описания процесса образования какого-либо продукта микроорганизмом, растущим на данном субстрате, можно вос­пользоваться уравнениями, аналогичными (6) и (7):

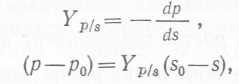(8), (9)

где Yp∕_s — коэффициент выхода продукта, dp — бесконечно ма­лое увеличение концентрации продукта, ро и р — соответственно исходная концентрация продукта и концентрация его в момент времени t.

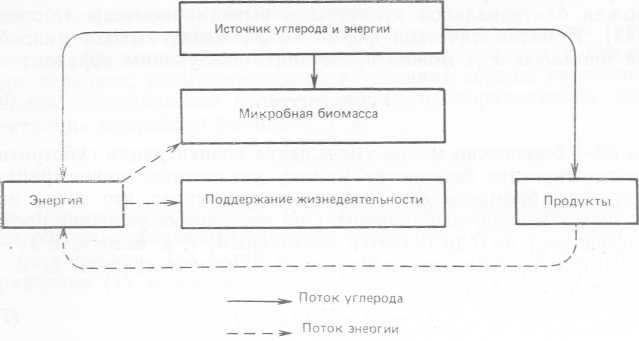
Рис. 10.1. Потоки углерода и энергии при гетеротрофнОхМ росте микробов и об­разовании продукта.

Для роста любого микроорганизма необходимы источники углерода и энергии. В случае гетеротрофных микроорганизмов это одно соединение или смесь углеродсодержащих соединений, которые удовлетворяют обе эти потребности. У автотрофных микроорганизмов углеродные и энергетические субстраты раз­личаются. Для гетеротрофных микроорганизмов и коэффициент выхода биомассы, и коэффициент выхода продукта зависят от распределения энергии и углерода между процессами анаболиз­ма и катаболизма. На рис. 10.1 представлена диаграмма рас­пределения потоков энергии и углерода при росте гетеротроф­ных микроорганизмов и образовании ими соответствующего продукта. Коэффициенты выходов зависят от природы источ­ника углерода и энергии, а также от биохимических особенно­стей данного микроорганизма; когда источник энергии и угле­рода подавляет рост, коэффициенты выхода зависят также и от его концентрации. В случае источника углерода и энергии с от­носительно высоким содержанием углерода (по сравнению с другими элементами) и, следовательно, с высокой энергетиче­ской константой при аэробном окислении наблюдается наруше­ние равновесия между высвобождением энергии и потреблением углерода; это ограничивает максимальный коэффициент выхода биомассы.

К этой категории углеродных энергетических субстратов от­носятся углеводороды. Избыточная энергия, высвобождаемая при их использовании, рассеивается в виде тепла и приводит к необходимости охлаждения микробиологических реакторов.

Скорость потребления определенного субстрата растущими культурами часто представляют в виде: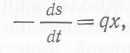 (10)

где q — метаболический коэффициент, который очень широко используется в микробиологии, особенно для кислорода и угле­родных энергетических субстратов. Подставив в это уравнение выражение для х из уравнения (1), получим: 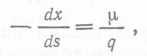  (11)  откуда с помощью уравнения (6) имеем:  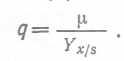 (12).

• 10.2.2. Кинетика роста и образования продукта

Экспоненциальная модель, описываемая уравнением (1), пред­ставляет собой лишь одну из нескольких относительно широко распространенных моделей роста микроорганизмов; каждая из таких моделей применима к специфическим физическим усло­виям или той или иной морфологии биомассы. Другими альтер­нативными моделями роста являются линейная модель и модель кубического корня. Первая из них относится к случаю, когда р®ст лимитируется диффузией субстрата или какого-либо пита­тельного вещества. Вторая модель часто применяется при опи­сании образования осадков (в случае плесневых грибов) или бактериальных хлопьев, которые разрастаются только по пери­ферии. На самом деле она представляет собой комбинацию модели экспоненциального роста и модели, в которой лимити­рующим фактором является перенос вещества. Модель кубиче­ского корня адекватно описывает образование мицелиальных осадков в периодической культуре, однако малопригодна для случая непрерывной культуры, поскольку не учитывает разру­шение хлопьев в биореакторе под действием гидродинамических сил.

Если для периодической культуры наблюдается экспоненци­альный рост, то это означает, что для широкого круга субстра­тов и в широком диапазоне их концентраций скорость роста фактически не зависит от концентрации субстрата. В этом слу­чае процесс роста следует кинетике нулевого порядка и можно ожидать, что потребление субстрата будет подчиняться следую­щему уравнению ферментативной кинетики:  (13), где qm— максимальный метаболический коэффициент при s^>Ks> Ks — константа насыщения, эквивалентная константе Михаэлиса—Ментен в ферментативной кинетике. Подставив вместо q и qm выражения, полученные из (12), мы придем к хорошо известному соотношению Моно: 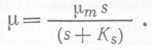 (14).

График этой функции представлен на рис. 10.2. Соотношение Моно широко используется не только потому, что дает универсальное описание кинетики роста микроорганизмов, но и бла­годаря своей простоте.

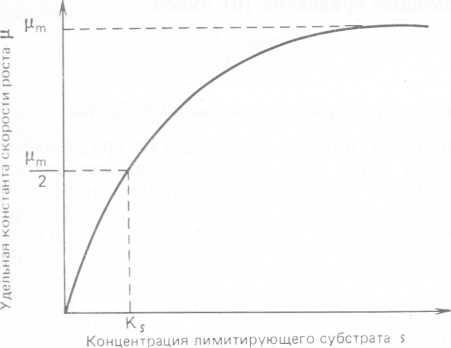
Рис. 10.2. Графическое представление соотношения Моно, описывающего зависимость удельной константы скорости роста от концентрации лимитирующего субстрата.

Для оценки μm и Ks (последняя из этих величин обратно пропорциональна сродству микроорганизмов к определенному субстрату) уравнение (14) можно преобразовать следующим образом: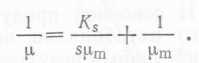 

Таким образом, график зависимосоти l∕μ от 1/s (т. е. график Лайнуивера — Бэрка) является прямой и пересекает ось абсцисс в точке —Ks, а ось ординат — в точке μm. Данных о значениях константы насыщения Ks очень немного. Для углеродных энергетических субстратов и для минеральных питательных веществ значение Ks обычно составляют ~10-s М, а для кислорода ~ IO-6—10~5 М.
Рост микроорганизмов (прирост биомассы) в промышленной установке можно описать с помощью уравнений (1), (14) и (7), к которым нужно еще добавить уравнения, описывающие потоки в реакторе:

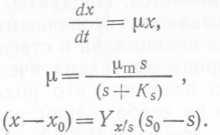
Если при этом происходит образование какого-то продукта, то нужно использовать еще и уравнение (9):

Однако образование микробных продуктов отнюдь не обязательно связано с ростом. Поэтому, прежде чем применять те или иные кинетические уравнения для анализа процессов в реакторе, необходимо установить, какая именно взаимосвязь существует между образованием продукта и ростом микроорганизмов.
Пожалуй, наиболее полезная классификация процессов образования продукта в периодических культурах была предложена более двадцати пяти лет назад Гэйденом (Gaden, 1959). Согласно этой классификации, все процессы можно разделить на три основные группы, которые обозначают как процессы типа I, II, III.
В процессах типа I основной продукт образуется в ходе реакций первичного энергетического метаболизма, когда между потреблением субстрата и образованием продукта существует постоянное стехиометрическое соотношение, метаболические пути представляют собой цепь последовательных реакций, а скорость любого процесса имеет один максимум, обычно совпадаю­щий с максимумом для других процессов. Типичными примерами процессов типа 1 служат образование этанола, глюконовой и молочной кислот из глюкозы, а также, разумеется, образование» микробной биомассы.

В процессах типа II основной продукт образуется в ходе реакций энергетического метаболизма непрямым путем: либо в ходе побочных реакций, либо в результате последующего вза­имодействия между прямыми продуктами метаболизма. Кине­тические кривые имеют сложный вид, причем максимумы ско­ростей различных процессов не совпадают. Типичными приме­рами процессов типа II являются образование лимонной и ита­коновой кислот, а также некоторых аминокислот.

К процессам типа III относятся те, в которых основной про­дукт образуется не в результате энергетического метаболизма, а независимым путем. В таких процессах рост и метаболическая активность достигают максимума на ранних этапах периодиче­ского процесса, а максимум образования интересующего нас продукта приходится на более поздние стадии, когда окисли­тельная активность снижается. Продукты, образующиеся в ходе таких процессов, называются вторичными метаболитами; это, например, антибиотики пенициллин и стрептомицин.

Три этих типа процессов схематически представлены на рис. 10.3. Совершенно очевидно, что подобная классификация была принята только из соображений удобства и не является ни совершенной, ни всеобъемлющей. Существуют процессы с совсем иными характеристиками, протекающие в средах раз­ного состава и при разных условиях. Отметим, что замена штам­ма мало сказывается на общем характере кинетических кривых. Впрочем, известны и исключения, особенно в процессах типа III. Это наводит на мысль, что по мере усложнения биосинтетиче­ских реакций, в ходе которых образуется данный продукт, дан­ный тип процессов можно подразделить на более мелкие классы.

Обратимся теперь к непрерывным микробиологическим про­цессам. Чтобы обеспечить протекание процесса в оптимальных условиях стационарного состояния, необходимо располагать со­ответствующими кинетическими данными. Если в условиях пе­риодической культуры процесс относился к типу I, то необходи­мые условия для непрерывного культивирования можно теорети­чески определить прямо из данных для периодического процесса. В целом процессы такого типа лучше всего протекают в стацио­нарных условиях в одностадийном биореакторе с полным пере­мешиванием. Те процессы, для которых в условиях периодиче­ской культуры характерны кинетики типа II или III, при не­прерывном культивировании, по всей видимости, лучше всего осуществлять в многостадийных последовательных биореактоpax. В этом случае можно так подобрать условия, чтобы ско­рость роста и связанный с ним энергетический метаболизм до­стигали максимума на одной стадии, а образование продукта — на другой. Прежде чем переводить такие процессы из периоди­ческих в непрерывные, очень важно выяснить соотношения меж­ду скоростями отдельных процессов и основными контролируе­мыми переменными.

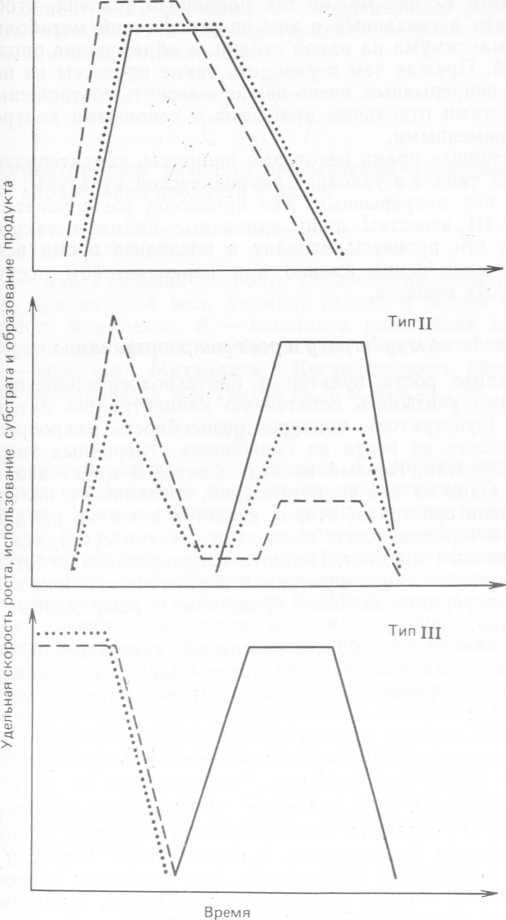
Рис. 10.3. Кинетические кривые для периодического процесса ферментации,  предложенные Гэйденом (Gaden, 1959). Штриховые кривые — рост, пунктир­ные— использование субстрата, сплошные — образование продукта.

В настоящее время некоторые процессы, характеризующиеся кинетикой типа I в условиях периодической культуры, осущест­вляются как непрерывные; для процессов же с кинетикой ти­па II и III известны лишь единичные примеры такого рода. Впрочем, эти процессы находят в последнее время все более широкое применение именно при периодическом поступлении питательных веществ.

• 10.2.3. Сродство к субстрату и рост микроорганизмов

При анализе роста культур в биотехнологических процессах необходимо учитывать остаточную концентрацию питательных веществ (субстратов), конкурентоспособность микроорганизмов- и особенности их роста на смешанных углеродных энергетиче­ских субстратах. Первый из этих факторов имеет два важных аспекта. Один из них экономический, связанный с полнотой ис­пользования субстрата; второй касается качества продукта, его чистоты и нетоксичности, поскольку остатки субстрата попада­ют в конечный продукт. Полнота использования субстрата, ко­торый является лимитирующим в периодической или непрерыв­ной культуре, определяется сродством к нему данных микро­организмов.

По-видимому, наиболее известной кинетической моделью ферментативных процессов является модель Михаэлиса — Мен­тен. Реакция фермента с субстратом описывается следующим уравнением: 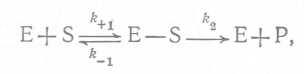 (16),

где E — фермент, S — субстрат, E—S - фермент-субстратный комплекс, P — продукт, ⅛+ι — константа скорости первой реак­ции в прямом направлении, k-↑— константа скорости первой реакции в обратном направлении, k₂— константа скорости вто­рой реакции, которая считается необратимой. Изменение кон­центрации фермент-субстратного комплекса описывается сле­дующим уравнением: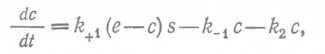 (17)

где е — концентрация фермента, с — концентрация фермент-субстратного комплекса, s— концентрация субстрата.

Если s3>e, то для стационарного состояния 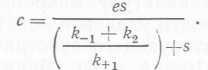 (18)
Для ферментативной реакции, описываемой уравнением (16), скорость образования продукта v равна 

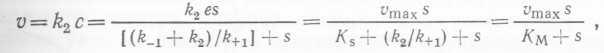 (19)

где υmax — максимальная скорость образования продукта, т. е. скорость, при которой весь фермент входит в состав фермент- субстратного комплекса, Ks — константа равновесия для реак¬ции диссоциации фермент-субстратного комплекса, KM,=KS + +k2∕k+↑ — константа Михаэлиса. Когда скорость образования продукта определяется константой k2, т. е. ⅛2⅛⅛+ι, то (20)

При выполнении условия (20) величина Км обратно пропорциональна сродству фермента к субстрату: чем меньше Км, тем выше сродство. Если мы заменим величины V, Omax и Км В (19) на μ, μm и Ks соответственно, то получим соотношение Моно (14), которое уже было введено нами ранее и графически представлено на рис. 10.2. Микроорганизмы, для которых кривая зависимости между μ и s имеет большой начальный наклон, обладают высоким сродством к лимитирующему субстрату. И наоборот, микроорганизмы, для которых эта кривая пологая, обладают низким сродством, и в таких культурах будут наблюдаться более высокие остаточные концентрации субстрата.
При непрерывном культивировании в хемостате конкуренция между двумя видами микроорганизмов за один лимитирующий субстрат определяется обычно именно их сродством к этому субстрату, а не максимальной удельной константой скорости роста μm. При стационарном режиме в простом хемостате без повторного использования биомассы концентрация лимитирующего субстрата равна 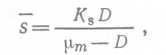  (21),

где D — скорость разбавления. Из этого соотношения видно, что концентрация лимитирующего субстрата в стационарном состоянии зависит от скорости образования клеток за счет роста, которая в точности равна скорости разбавления, и от параметров, характеризующих рост данного микроорганизма. Ясно, что па­раметры, характеризующие рост разных микроорганизмов на одном и том же субстрате, вряд ли будут одинаковы. Предпо­ложим, что мы имеем культуру микроорганизмов А и В. По-, строив график зависимости удельной константы скорости роста μ от концентрации лимитирующего субстрата s, мы получим два разных случая (рис. 10.4, А и Б).

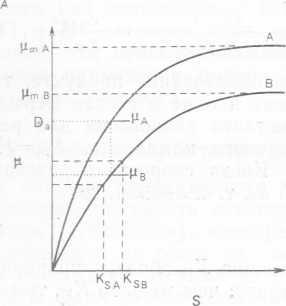
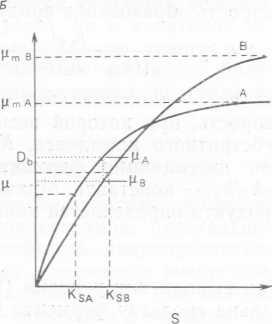
В ситуации, изображенной на рис. 10.4, А, для микроорганизма А при любой данной ско­рости разбавления (скорости роста) будет наблюдаться более низкая концентрация лимитирующего субстрата, чем для мик­роорганизма В при той же скорости разбавления (скорости роста). Следовательно, в хемостате, где рост двух видов мик­роорганизмов А и В лимитируется одним и тем же субстратом, А всегда будет вытеснять В, поскольку последний не способен сохранять достаточно высокую скорость роста при той концент­рации субстрата, которая наблюдается для вида А, даже если максимальная удельная скорость роста для В не была превы­шена. Напротив, в ситуации, изображенной на рис. 10.4, Б, отно­сительная конкурентоспособность двух видов микроорганизмов, растущих в хемостате на одном лимитирующем субстрате, будет зависеть от степени разбавления. Подобный анализ конку­рентного роста в хемостатах можно распространить и на много­компонентные смешанные микробные популяции, однако такая экстраполяция не всегда оказывается возможной, поскольку в сложных смешанных культурах могут существовать несколько другие взаимоотношения. Кроме того, в смешанных культурах, применяющихся в биотехнологических процессах, использовать основной субстрат обычно может только один вид микроорга­низмов из всех присутствующих, а другие лишь модифицируют среду с тем, чтобы оптимизировать рост основного вида, осо­бенно если этот последний слишком прихотлив.

Вообще говоря, любой гетеротрофный микроорганизм спосо­бен расти на самых разных субстратах — источниках углерода и энергии. Большинство углеводов служат субстратом для очень широкого спектра микроорганизмов; для углеводородов этот спектр уже; на некоторых синтетических органических соедине­ниях способны расти лишь очень немногие микроорганизмы, а большинство таких соединений вообще не могут служить субстратами. Один из основных вопросов, касающихся исполь­зования смешанных субстратов данным гетеротрофным штам­мом, состоит в том, как расходуются эти субстраты — одновре­менно (конкурентным образом) или последовательно.

Для периодической чистой культуры микроорганизмов, рас­тущей на смеси двух субстратов, обычно наблюдается так назы­ваемый диауксичный рост. При этом на кинетической кривой выявляются две четко различимые экспоненциальные фазы, разделенные интервалом, на котором скорость роста проходит через минимум. Такой характер роста обусловлен последова­тельным использованием субстратов. Диауксичный рост на са­харах впервые наблюдал Моно в 1942 г., однако подобная кар­тина имеет место и для других субстратов. Диауксичный рост характеризуется тем, что микроорганизмы не способны синте­зировать ферменты, необходимые для метаболизма второго углеродного субстрата, несмотря на его наличие, т. е. индукции не происходит даже в присутствии индуктора. Это явление получило название катаболитной репрессии.

При росте периодических культур на двухкомпонентном субстрате наблюдаются и другие явления. Субстраты могут использоваться независимо, так что потребление одного не сказывается на потреблении другого. В таком случае они могут метаболизироваться одновременно, и при этом иногда наблю­дается даже стимуляция роста. Возможны ситуации, когда ферменты, необходимые для метаболизма второго субстрата, синтезируются, но их активность ингибируется, и тогда суб­страты используются последовательно, но рост, строго говоря, не является диауксичным. В случаях двухкомпонентных смесей последовательно используемых субстратов тот субстрат, кото­рый метаболизируется быстрее, обычно расходуется первым, хотя известны и исключения. Однако в каждой конкретной двух­компонентной смеси субстратов быстрее может использоваться то один, то другой субстрат в зависимости от того, какой микро­организм растет на этой смеси.

В связи со всем сказанным выше важно отметить, что мно­гие культуральные среды, применяющиеся в промышленных биотехнологических процессах, представляют собой сложные смеси субстратов и их состав влияет на производительность процесса. Характер потребления смешанных субстратов в не­прерывных проточных культурах не всегда можно предсказать исходя из результатов, полученных на экспериментальных установках с периодическими культурами, растущими на таких же смесях субстратов. В непрерывных проточных системах компоненты смеси могут потребляться одновременно, даже если в периодической культуре того же микроорганизма они исполь­зовались последовательно. Особый интерес представляет сле­дующее наблюдение, сделанное на хемостатной культуре. Ока­залось, что в двухкомпонентной смеси субстратов критическая скорость разбавления для полного использования того компо­нента, который обеспечивает более медленный рост периодиче­ской культуры, может значительно превышать нормальную скорость вымывания. Кроме того, применяя двухкомпонентные смеси субстратов в непрерывной культуре, можно контролиро­вать поступление углерода в те или иные метаболические пути, изменяя состав субстратной смеси или условия протекания про­цесса, и регулировать тем самым количество образующейся энергии или какого-либо продукта.

• 10.2.4. Стабильность культуры и требования, предъявляемые ею

Пригодность выбранной культуры для использования ее в дан­ном промышленном микробиологическом процессе часто не оценивается и становится критическим фактором, когда дело доходит до практического ее применения. Совершенно очевидно, что, вообще говоря, самое главное — это генетическая стабиль­ность культуры, но обсуждение вопросов этого круга выходит за рамки данной главы. Здесь в общих чертах мы рассмотрим физические, химические и пищевые факторы, а также требова­ния, предъявляемые микроорганизмами. Основные условия, необходимые для роста микроорганизмов, были перечислены выше, но всегда остается вопрос: обеспечивают ли выбранные условия оптимальный рост и/или образование продукта? К ка­ким последствиям могут привести изменения этих условий, в частности, как это скажется на продуктивности процесса?

Теплопередача и перенос веществ в биореакторах увеличи­ваются за счет диссипации энергии в системе, обычно в резуль­тате интенсивного механического перемешивания содержимого реактора вращающимися мешалками. Такие мешалки оказыва­ют двоякое действие: способствуют диспергированию мелких пузырьков воздуха в толще культуральной среды и обеспечива­ют перемешивание, необходимое для минимизации концентраци­онных градиентов, эффективного охлаждения реактора и умень­шения выделения пузырьков воздуха. Однако возникающие при таком перемешивании гидродинамические силы могут повреж­дать клетки, особенно в случае волокнистых плесневых грибов,, актиномицетов, бактерий, имеющих жгутики, фимбрии, а так­же хрупких клеток тканей, выращиваемых в суспензионной куль­туре. Образование специфического продукта может зависеть от морфологии плесневого гриба; по этой причине явно непригод­ны для использования в промышленных процессах те штаммы,, морфология которых значительно изменяется при изменении условий культивирования. Кроме того, следует избегать таких условий проведения процесса, когда мицелий плесневых грибов повреждается.

Ранее считалось, что вероятность повреждений бактериаль­ных клеток определяется скоростью вращения лопастей мешал­ки. Однако, согласно наиболее правдоподобной современной гипотезе о механизме повреждений, они обусловлены кавитаци­онными явлениями в вихрях, возникающих сразу за лопастями мешалок. Вопрос о повреждении бактериальных клеток в интен­сивно перемешиваемых культурах все еще не решен. Если анализировать свойства суспензий бактериальных клеток в по­токе, используя для определения гидродинамических характе­ристик любой отдельной бактериальной клетки предположение, что она представляет собой сферическую частицу соответствую­щего диаметра, то оценить силы, вызывающие механическое повреждение клетки, не удается. Подобный подход не учиты­вает наличие жгутиков или фимбрий: они — особенно это каса­ется жгутиков — могут в несколько раз превосходить по длине самые крупные несущие их бактериальные клетки. Вполне воз­можно, что именно разрыв этих структур и последующее выте­кание клеточного содержимого ответственны за разрушение клеток при интенсивном перемешивании бактериальных куль­тур. Заметим, что значительная часть исследований по генети­ческой инженерии направлена на осуществление передачи специфических свойств от различных бактерий к Escherichia coli, которая не особенно пригодна для использования ее в процессах с интенсивным перемешиванием именно из-за нали­чия фимрий и жгутиков и, следовательно, подверженности ме­ханическим повреждениям.

Если среди плесневых грибов и бактерий, вероятно, можно отобрать выносливые микроорганизмы, более или менее при­годные для использования их в условиях, характерных для интенсивных процессов, то культуры тканей, в частности куль­туры клеток млекопитающих, нуждаются в особых биореакто­рах, конструкция которых учитывает присущую этим клеткам хрупкость.

Если говорить о других условиях среды, то совершенно очевидно, что наиболее пригодны для использования в промыш­ленности микроорганизмы с широкими диапазонами оптимумов pH, концентрации растворенного кислорода и температуры. Впрочем, частично эти трудности позволяют обойти техниче­ское усовершенствование установок и улучшение контроля за условиями в них. Отметим, однако, что в некоторых новых конструкциях промышленных биореакторов, в частности в ко­лонных аппаратах и в циклических системах под давлением, создаются значительные градиенты как физических параметров, так и концентраций питательных веществ. Если экономические преимущества подобных систем над более привычными доста­точно велики, то для достижения высокой экономичности про­цесса в целом крайне важно, чтобы в нем принимали участие микроорганизмы, сохраняющие высокую продуктивность в быст­ро меняющихся условиях.

В заключение следует отметить, что в последнее время не уделялось достаточно внимания использованию в промышлен­ных биотехнологических процессах смешанных, неприхотливых культур определенного состава. Впрочем, даже в процессах, осуществляемых при участии таких культур, значительные из­менения условий могут приводить к нарушению равновесия в соотношении между разными микроорганизмами, составляющи­ми эти смешанные популяции.