Любой процесс, в котором участвуют микроорганизмы, незави­симо от способа его осуществления можно отнести к одной из двух категорий, определяемой характером поставленной задачи: 1) получение нужных микроорганизмов; 2) осуществление опре­деленных химических превращений.

Последний тип процессов можно подразделить еще на два класса: а) получение нужного конечного продукта; б) перера­ботка сырья.

Все процессы, осуществляемые с целью химического превра­щения, обладают одной общей особенностью, резко отличающей их от процессов, цель которых — получение микробной биомас­сы: микроорганизмы, осуществляющие данное превращение, не обязательно должны при этом находиться в состоянии роста. Этот аспект нередко недооценивается, хотя общеизвестно, что химические превращения могут осуществляться даже микроор­ганизмами, уже потерявшими жизнеспособность. За такие превращения ответственны клеточные ферменты. Совершенно очевидно, что для контролируемого осуществления многих пре­вращений с самым высоким выходом лучше всего использовать иммобилизованные покоящиеся клетки или иммобилизованные ферменты, выделенные из этих клеток. Роль таких систем при проведении некоторых превращений в промышленных масшта­бах становится все больше, однако при этом возникают про­блемы, связанные со стабильностью подобных биокаталитиче- ских систем, регенерацией кофакторов и с диффузией. Наиболее широко применяемой в промышленных масштабах техноло­гией остается химическое превращение, осуществляемое расту­щими культурами микроорганизмов. C биохимической точки зрения микробиологические процессы можно подразделить на две основные категории: катаболические, в ходе которых слож­ные соединения расщепляются до более простых, и биосинтети­ческие, в ходе которых сложные соединения образуются из бо­лее простых.

В основе любого процесса, протекающего при участии мик­роорганизмов, лежит та или иная реакция или последователь­ность реакций. Тем не менее при реализации этого процесса в промышленном масштабе лимитирующим фактором, как пра­вило, оказывается не кинетика этой реакции или последователь­ности реакций, а другой, на первый взгляд менее существенный фактор, который и определяет возможности использования дан­ного процесса в промышленности.

Ключевыми факторами, влияющими на экономичность про­цесса в биореакторе, являются производительность и степень превращения, а они в свою очередь определяются теми физиче­скими факторами, от которых зависит теплопередача и перенос массы. К этим факторам относятся: 1) гидродинамические свойства суспендированных микроорганизмов; 2) реологические свойства культуральных сред; 3) электрокинетические свойства микроорганизмов; 4) давление; 5) поверхностные и пристеноч­ные эффекты, а также эффекты, возникающие на границе раз­дела фаз; 6) эффекты, связаные с наличием нескольких фаз в потоке; 7) флотационные, седиментационные и сегрегацион­ные эффекты.

Интересно было бы обсудить, какую же реальную информа­цию о любом из этих факторов и/или их влиянии на рост мик­роорганизмов или на образование продукта могут дать микро­биологические исследования процессов, протекающих с участием микроорганизмов.

• 10.3.1. Классификация биореакторов и их производительность

Химические реакции можно классифицировать по-разному. Если иметь в виду выбор конструкции реактора, то, вероятно, наиболее полезной будет классификация, основанная на том,, в однофазной или в многофазной среде протекает данная реак­ция. Реакции, идущие в однофазной среде, называются гомоген­ными, а в многофазных —гетерогенными. Для большинства ферментативных реакций и многих реакций, протекающих при участии микроорганизмов, подобная классификация не являет­ся однозначной, поскольку они занимают весьма обширную' область между гомогенными и гетерогенными реакциями. Чтобы упростить классификацию биохимических реакций, условились считать реакционные системы, в которых существуют только микроградиенты концентраций, гомогенными, а системы с мак­роградиентами— гетерогенными. Следовательно, для биохими­ческих реакций понятия гомогенности и гетерогенности не совпа­дают с таковыми для химических реакций.

Любую систему, у которой существует ограничивающая ее поверхность и в которой протекают биохимические реакции, можно назвать биореактором. Промышленный биореактор — это емкость, в которой осуществляются рост микроорганизмов и/или различные химические превращения.

Промышленные биореакторы могут работать в периодиче­ском режиме, периодическом режиме с доливом субстрата, полунепрерывном (полупериодическом) и непрерывном проточ­ном режимах. Исторически в промышленности утвердился периодический способ работы при осуществлении химических превращений и полунепрерывный — при получении микробной биомассы. В последнее время для химических превращений ста­ли применять реакторы с периодическим режимом и с доливом субстрата, а для получения микробной биомассы — реакторы, работающие в непрерывном проточном режиме. Традиционно биореакторы, работающие в непрерывном проточном режиме, использовались в промышленном масштабе только для аэробной переработки сточных вод и отходов (т. е. в процессах с самой большой пропускной способностью среди всех технологических операций), а также при производстве уксуса. За исключением этих двух случаев, биологическая промышленность проявляла исключительный консерватизм в том, что касалось перехода на непрерывную проточную технологию, причем без достаточных на то оснований.

Детальный анализ некоторых потенциальных режимов рабо­ты биореакторов указывает на превосходство проточного непре­рывного режима. При работе по периодическому режиму в ре­актор загружают все необходимые компоненты (за исключением кислорода для аэробных процессов), ведут процесс до конца и собирают конечный продукт. Периодический режим с добавлением субстрата предусматривает периодическое или не­прерывное введение субстрата без удаления конечного продукта, который собирают только по завершении процесса. При полу­непрерывном ведении процесса, который называют также полупериодическим, по завершении начальной стадии в перио­дическом режиме реактор наполовину опорожняют, чтобы час­тично собрать продукт, а затем снова заполняют таким же объемом свежей среды и доводят процесс до конца; затем снова осуществляют ту же последовательность операций. По­добный подход направлен на лучшее использование производ­ственной установки.

Сравним производительность реактора, работающего в периодическом и непрерывном проточном, с идеальным переме­шиванием, режимах. Периодический процесс включает несколь­ко этапов: подготовительный, лаг-период, фазу экспоненциаль­ного роста и период удаления продукта; с точки зрения производительности реактора важен только период экспонен­циального роста. Время, необходимое для завершения цикла t_ц, можно представить как сумму продуктивного времени t и общего непродуктивного времени tн, т. е.   (22)

Из уравнения (3), имея в виду, что для экспоненциального рос­та μ==μ_m, получаем 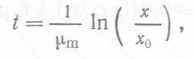 (23), 

так что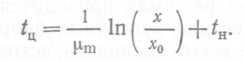 (24)

Для периодического процесса общая продуктивность равна суммарной продукции, деленной на полное время цикла. Сум­марная продукция задается соотношением (7), но для таких периодических процессов, которые мы рассматриваем, остаточ­ная концентрация субстрата s фактически равна нулю. Следо­вательно, суммарная продукция равна

(25),   производительность периодического процесса P_a составляет 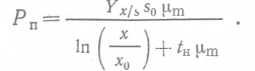 (26).

По определению производительность реактора (выход биомас­сы), работающего в непрерывном проточном режиме с идеаль­ным перемешиванием, равна   (27)

где х — концентрация биомассы в реакторе в стационарном состоянии. Если принять, что коэффициент выхода биомассы Y_x∕_s и концентрация субстрата в свежей среде S₀ для периоди­ческого и непрерывного процессов одинаковы, а S — остаточная концентрация лимитирующего субстрата, то уравнение (27) имеет вид 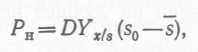 (28),  откуда при s≪ s₀ получаемP_b = DY_x,_ss₀.  (29) .  

Следовательно, отношение производительностей равно 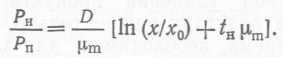 (30)

В реакторе, работающем в проточном непрерывном режиме с полным перемешиванием, максимальная скорость разбавления равна D = μ_m. Однако во избежание нестабильности на самом деле поддерживают скорость разбавления на уровне 0,8 μ∏_b, и тогда 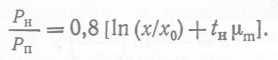 (31)

Графическое сопоставление продуктивности реактора в периоди­ческом и непрерывном режимах приводится на рис. 10.5.

Рабочие характеристики проточных биореакторов непрерыв­ного действия лучше всего оценивать исходя из расчета мате­риального баланса по биомассе, лимитирующему субстрату и продукту. Используя самую приближенную классификацию проточных биореакторов непрерывного действия с суспензион­ными культурами, можно выделить два типа реакторов: реак­торы с идеальным перемешиванием и проточные биореакторы в режиме полного вытеснения (реакторы поршневого типа). Биоре­акторы с идеальным перемешиванием могут работать как хемо­статы или как турбидостаты. В хемостате поддерживается постоянная плотность микробной культуры за счет потребления лимитирующего субстрата или какого-либо иного питательного вещества, а в систему турбидостата входит светочувствительное устройство, которое измеряет оптическую плотность культуры и обеспечивает ее постоянство.

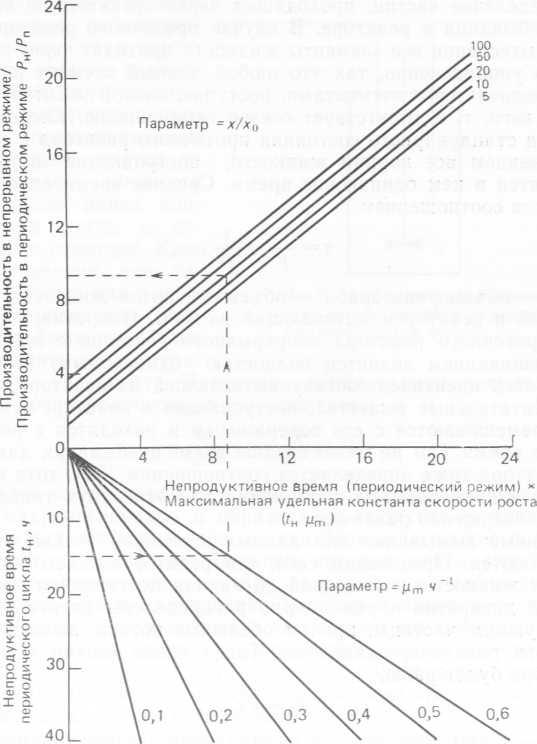
Рис. 10.5. Соотношение между образованием микробной биомассы в реакторе, работающем в непрерывном и периодическом режимах, для различных коли­честв посевого материала, максимальных удельных констант скорости роста и продолжительностей непродуктивного этапа периодического цикла; D = 0,8 μ_m для непрерывной системы (Aiba et al., 1973).

В промышленности, как правило, применяются реакторы, работающие в режиме хемостата, поэто­му о турбидостатах мы далее говорить не будем.

Любой анализ производственных характеристик биореактора включает изучение свойств существующих в нем потоков, а так­же кинетики роста микроорганизмов и осуществляемых с их участием превращений. Для описания потока в проточном ре­акторе непрерывного действия удобнее всего использовать
распределение частиц, проходящих через реактор, по времени их пребывания в реакторе. В случае проточного реактора пол­ного вытеснения все элементы жидкости проходят через реактор строго упорядоченно, так что любой данный элемент никак не перемешивается с элементами, поступающими в реактор до или после него, т. е. отсутствует осевое перемещение. Следователь­но, для стационарного состояния проточного реактора с полным вытеснением все порции жидкости, поступающие в реактор, находятся в нем одинаковое время. Среднее время пребывания задается соотношением   (32),

где V — объем реактора, F — объемный поток жидкости, посту­пающий в реактор и вытекающий из него. Напротив, содержи­мое проточного реактора непрерывного действия с идеальным перемешиванием является полностью однородным, а потому его состав идентичен составу вытекающей из реактора жидко­сти. Питательные вещества, поступающие в реактор, немедлен­но перемешиваются с его содержимым и находятся в реакторе разное время. Тем не менее среднее время пребывания для тако­го реактора тоже определяется соотношением (32), хотя кривые распределения времени пребывания для этих двух типов реак­торов совершенно различны.

Кривые вымывания для данных реакторов также сильно различаются. Представим себе, что реактор каждого типа на­полнен жидкостью, в которой до начала поступления новых ее порций дискретно и равномерно распределены инертные, несе­грегирующие частицы, причем объемные потоки, выходящие из каждого реактора, одинаковы. Тогда число частиц в каждом реакторе будет равно 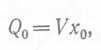 (33) , где V—объем жидкости, X₀ — начальная концентрация. При поступлении в реактор новых порций чистой жидкости из него будет вытекать поток (обеспечивающий постоянство объема содержимого реактора), концентрация твердых частиц в кото­ром будет неодинакова для разных типов реакторов. При этом число частиц, остающихся в реакторах, будет непрерывно умень­шаться.

Для идеального проточного реактора с полным вытеснением концентрация частиц в вытекающей жидкости будет равна хо до тех пор, пока время вытекания t не станет равно времени пребывания τ; в этот момент х станет равным нулю. Число частиц, остающихся в реакторе, будет линейно уменьшаться во времени и при t=τ станет равным нулю. Для реальных проточных реакторов с полным вытеснением наблюдает­ся несколько иная карти­на из-за осевого переме­шивания и диффузии. Для реакторов с пол­ным перемешиванием концентрация частиц в вытекающей жидкости всегда будет равна кон­центрации частиц в со­держимом реактора. Кри­вая вымывания для таких реакторов, как и кри­вая распределения вре­мени пребывания, будет представлять собой отри­цательную экспоненту. 

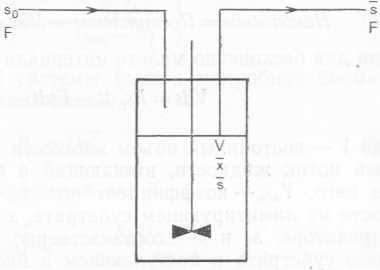
  Рис. 10.6. Проточный биореактор не­прерывного действия с полным пере­мешиванием (см. текст).

Изменение концентрации частиц и их числа в реакторе описываются уравнением 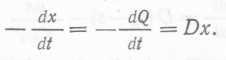 (34)

Используя соотношения для скорости вымывания, уравнения роста микроорганизмов и образования продукта, а также выражение для коэффициентов выхода биомассы, можно получить уравнения материального баланса, которые описывают работу идеального проточного реактора непрерывного действия. Для этого нужно найти соотношение, в котором накопление какого- либо продукта выражено через увеличение его количества благодаря входящему потоку, уменьшение из-за вытекающего потока, увеличение за счет роста или образования продукта в реакторе, уменьшение за счет использования в реакторе и увеличение за счет рециркуляции потока.
Уравнение материального баланса для биореактора, рабо-тающего в проточном режиме с идеальным перемешиванием без рецикла, т. е. обычного хемостата (рис. 10.6), где продуктом служит только микробная биомасса, выглядят следующим образом.

Для микробной биомассы
Накопление = Рост — Удаление

или для бесконечно малого интервала времени

(35)

Для лимитирующего субстрата

Накопление = Поступление—Удаление—Использование

или для бесконечно малого интервала времени dt

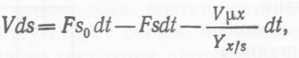 (36)

где V — постоянный объем жидкости в биореакторе, F — объем­ный поток жидкости, втекающий в биореактор и вытекающий из него, Y_x∕_s — коэффициент выхода микробной биомассы при росте на лимитирующем субстрате, х — концентрация биомассы в реакторе, Sо и s — соответственно концентрации лимитирую­щего субстрата в поступающем в биореактор растворе и в ре­акторе, μ — удельная константа скорости роста.

Разделив (35) и (36) на Vdt, получим 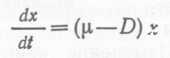 (37)  и  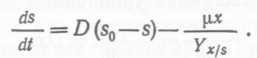(38).

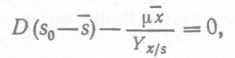В стационарном состоянии dx/dt = Q и ds/dt=Q. Следовательно, (39), откуда  (40) , и таким образом (41)

где х π s — соответственно концентрации микробной биомассы и лимитирующего субстрата в стационарном состоянии.

Соотношение Моно можно переписать следующим образом: 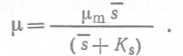(42) 

Отсюда можно получить выражение для концентрации лимити­рующего субстрата в стационарном состоянии, заменив μ на D: 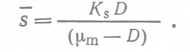  (21)

Концентрацию бактеральной биомассы в стационарном состоя­нии получим, заменив сначала в уравнении (41) μ на D, а за­тем подставив выражение (21) для S

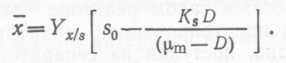 (43)

Производительность такой системы (выход микробной биомассы) в стационарном состоянии равна  (27)

или, после подстановки выражения для х 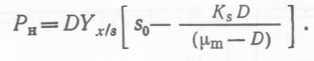 (44)

Графики зависимости х, s и Pa от скорости разбавления D, построенные в соответствии с соотношениями (43), (21) и (27), приведены на рис. 10.7.

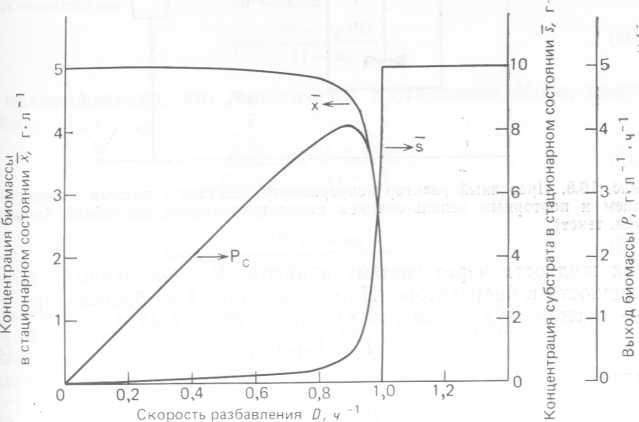
Рис. 10.7. Теоретическая зависимость концентрации биомассы, концентрации лимитирующего субстрата в стационарном состоянии, выхода микробной биомассы от скорости разбавления для простого хемостата (μtn=l,0 ч-1, Ks= = 0,1 г-л-1, 7x∕s=0,5, S0=IO г-л-*).

Найдем уравнения материального баланса для другой системы — проточного реактора непрерывного действия с полным перемешиванием, единственным продуктом которого является микробная биомасса; в таком реакторе для интенсификации процесса часть концентрированной микробной биомассы ис­пользуется повторно, поступая из сепаратора, расположенного на выходе из реактора (это может быть седиментационный тэнк, применяемый при очистке сточных вод; центрифуга или система ультрафильтрации). В подобной системе, изображенной на рис. 10.8, скорость разбавления D равна F/V, где F — поток жидкости через систему в целом, V — постоянный объем жидкости в биореакторе. 

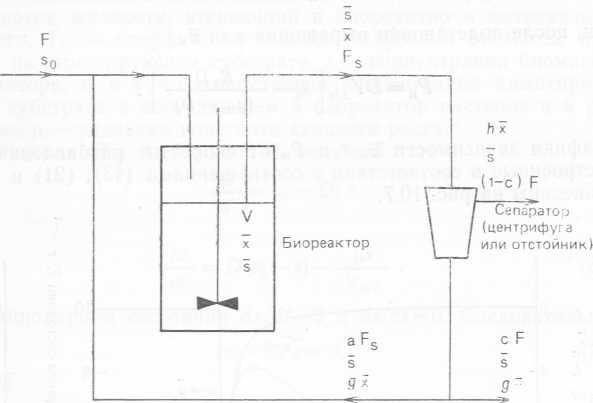
Рис. 10.8. Проточный реактор непрерывного действия с полным перемешиванием и повторным использованием концентрированной микробной биомассы (см. текст).

Поток, выходящий из биореактора (но не из системы в целом), можно представить в виде 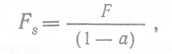  (45) или  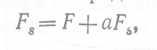(46), где а — доля вытекающего из реактора содержимого, которая используется повторно. Если принять, что микробная биомасса становится более концентрированной в g раз, то количество биомассы, повторно используемой в биореакторе, будет равно aFsgx. Уравнение материального баланса по биомассе будет в этом случае иметь вид

Накопление = Рост—Удаление + Повторное использование,

или для бесконечно мялпгп интепвяля впемени dt

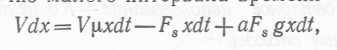(47),

а соответствующее уравнение по лимитирующему субстрату —

Накопление = Поступление + Повторное использование—Удаление— — Расходование,

или для малого интервала времени

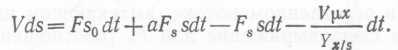 (48)

Подставив в (47) выражение для Fs и разделив на Vdt, мы получим для стационарного состояния (при котором dx/dt=G): 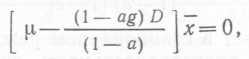  (49)

В предположении, что выполняется соотношение Моно, полу­чаем 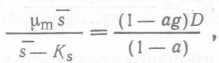 (51) или  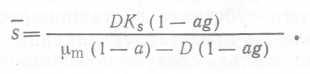(52).

Подставив в (48) выражение для F_s и разделив на Vdt, мы по­лучим для стационарного состояния (при котором ds∕dt=Q) уравнение, которое представляет собой уравнение для обычного хемостата (41). Подставив в него выражение для $, будем иметь 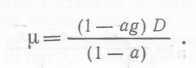 (53)

Для определения концентрации микробной биомассы hx в ос­ветленном потоке, вытекающем из сепаратора, нужно найти уравнение материального баланса по биомассе в сепараторе. В предположении, что сепаратор работает в стационарном ре­жиме, т. е. биомасса в нем не накапливается, уравнение ма­териального баланса для биомассы можно записать следую­щим образом:

Поступление — Повторное использование + Концентрированные от­ходы + Осветленные отходы

или

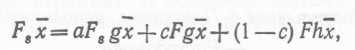(54)

где с — доля потока F, вытекающего из системы в виде кон­центрированных отходов, h — концентрационный коэффициент по биомассе в осветленном потоке, вытекающем из сепаратора.

Если реактор работает в стационарном режиме, то его произво­дительность (но не производительность системы в целом) по биомассе будет равна 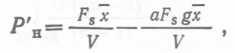(56) или, после замены F_a,  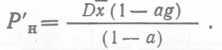(57).

Зависимость между производительностью P'_κ, концентрацией микробной биомассы в стационарном состоянии х, концентра­цией лимитирующего субстрата в стационарном состоянии $ и скоростью разбавления представлена на рис. 10.9. Из этих со­отношений с очевидностью следует потенциальная возможность увеличения рабочей скорости разбавления или благодаря пов­торному использованию биомассы, как в рассматриваемом на­ми случае, или путем удержания активной биомассы.

Вернемся теперь к анализу работы проточного биореактора с полным вытеснением. В этом случае в каждом малом эле­менте жидкости dυ, проходящем через биореактор, имеет ме­сто в основном экспоненциальный рост (μ = μ_m), если только концентрация первого лимитирующего субстрата значительно превышает константу насыщения K_s. Рост биомассы в таком биореакторе без рецикла описывается следующим уравнением: Inx= In x₀ -∣- μ_m t,  (58), где X₀ — концентрация биомассы в среде, поступающей в био­реактор, х — концентрация в момент времени t.

Если v — объем культуральной среды, вышедшей из биореактора за время t, то t≈υ∣F=υ∣Vd. Подставив это выражение для t в уравнение (58), получаем  (59).

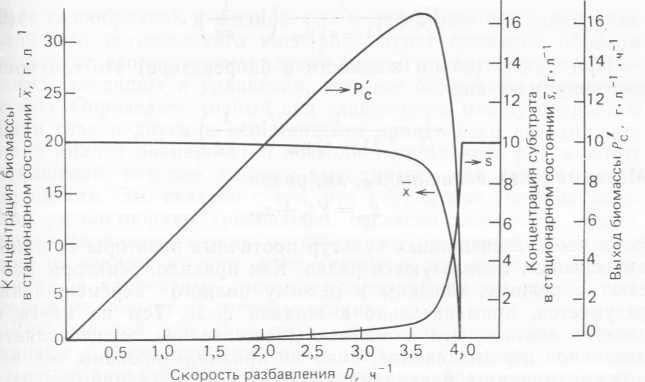
Рис. 10.9. Теоретическая зависимость концентрации биомассы и лимитирующего субстрата в стационарном состоянии, а также выхода микробной биомассы в биореакторе от скорости разбавления для хемостата с концентрированием микробной биомассы и ее повторным использованием (μm=l,0 ч-1, Ks= = 0,1 г-л-1, yx∕s=0,5, S0= 10 г-л-1, α=0,2, g=4).

При рециркуляции микробной биомассы в проточном биореак­торе с полным вытеснением никакой внешней инокуляции не требуется. В подобной системе общий поток, вытекающий из биореактора (но не из всей системы), описывается уравнением (46), как и в случае рассмотренного выше реактора с рецирку­ляцией. Если биомасса концентрируется в сепараторе в g раз, то доля ее, повторно используемая в биореакторе, будет равна ag. Если x_w — концентрация биомассы в потоке, вытекающем из биореактора, то в стационарном состоянии x₀ = agx_w. Время /, за которое из реактора вытечет объем V, равно  (60).

Приняв υ =V_h — объему, при котором происходит исчерпание лимитирующего субстрата, и заменив х и t в уравнении (59), для стационарного состояния получим

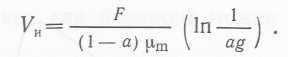 (61).  

При V_a = V (объем жидкости в биореакторе) это соотношение принимает вид 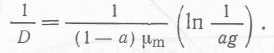 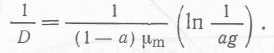 (62). 

Максимальная величина xw, хт, равна  (63).

В случае суспензионных культур проточные реакторы с полным вытеснением используются редко. Как правило, реакторы работают в режиме, близком к режиму полного перемешивания, разумеется, применительно к жидкой фазе. Тем не менее нe следует считать, что в системе действительно осуществляется идеальное перемешивание, пока не проанализированы все возможные причины появления неоднородности (например, из-за пристеночного роста и т. п.). Вероятно, самым лучшим приближением к реактору с полным вытеснением был бы каскад последовательных реакторов с идеальным перемешиванием без дополнительных поступлений питательных веществ, однако для этого число биореакторов, составляющих такой каскад, должно быть бесконечным. Неидеальный поток с полным вытеснением можно получить, лишь когда работает более шести последовательных биореакторов.

• 10.3.2. Анализ размерностей и масштабирование

Анализ размерностей и моделирование с помощью безразмерных величин широко применяются в химической технологии и не менее важны для конструирования биореакторов и их масштабирования. C анализом размерностей и с безразмерными величинами хорошо знакомы лишь немногие микробиологи. Это прежде всего метод, с помощью которого можно получить, какую-то информацию о взаимосвязях между переменными, характеризующими определенные физические системы. Ценность такого подхода состоит в том, что его можно применять в тех случаях, когда мы располагаем неполной информацией о системе, и тогда получаемая частичная информация нередко имеет большую ценность, позволяя уменьшить число экспериментов, необходимых для получения полной информации.
Рассмотрим, например, физическую абсорбцию кислорода1 в аэрируемом биореакторе. Очевидно, что для полного описания системы с физической точки зрения необходимо вывести сложные гидродинамические уравнения, описывающие перемещение газообразной и жидкой фаз и диффузию в жидкой фазе. Количество поглощенного кислорода будет сложным образом зависеть от скорости поступления газа и от всех других пере­менных, входящих в уравнения, которые описывают перемеще­ние фаз. Определить точный вид зависимости между скоростью подачи газа и другими переменными практически невозможно; однако анализ размерностей позволяет установить ряд важных соотношений, которые должны выполняться для любой такой зависимости. Это связано с тем, что корректные способы изме­рений удовлетворяют требованию, согласно которому число, равное отношению между результатами измерений двух объ­ектов, не зависит от того, какая единица используется для из­мерений, а корректные системы уравнений имеют такой вид, который не зависит от системы единиц.

Решение той или иной технологической проблемы обычно начинают с очень приближенного анализа, учитывая как мож­но меньше деталей. В результате исходные характеристики про­цессов, протекающих в реакторе, могут быть представлены в виде простого соотношения между двумя или тремя безразмер­ными величинами и соответствующими эмпирическими констан­тами. Существует около трехсот безразмерных величин, пред­ставляющих интерес с точки зрения технологии, но на самом деле большинство биотехнологов имеют дело только с двумя десятками.

Наиболее широко используемая безразмерная величина — это число Рейнольдса N-Re, которое применяется при описании потока жидкости: 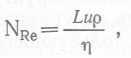 (64).

где L — характеристический размер, и — скорость потока, р — плотность жидкости, η — ее вязкость. При конструировании биореакторов числа Рейнольдса используются при описании по­тока жидкости в трубопроводах, движения капель, частиц и пузырьков газа, а также вращающихся мешалок. Для потока жидкости в трубопроводе

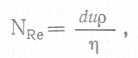 (65), 

где d — диаметр трубопровода, и — скорость потока. Для ча­стиц, пузырьков или капель, погружающихся в жидкости или всплывающих в ней,

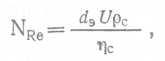 (66), 

где d₃ — эквивалентный диаметр частиц, пузырька или капли, т. е. диаметр сферы, равной по объему частице, пузырьку или капле, U — скорость частицы, всплывающей или погружающей­ся в жидкость, ,ре — плотность среды, η_c — ее вязкость. Для вращающихся мешалок

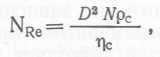 (67) ,

где D — диаметр перемешивающего устройства, N — скорость вращения.

Перечислим некоторые другие безразмерные величины, обычно используемые химиками-технологами: число Нуссель­та Nnu, число Прандтля Np_r, число Гразгофа Ngγ, число Фруда N_fγ, число Пекле N_Pe, число Стэнтона Nst, число Шмидта Nsc число Шервуда Nsh, число Вебера Nwe.  Как и число Рейнольд­са, некоторые из этих величин имеют по нескольку определе­ний, а, например, числа Пекле, Прандтля и Нуссельта записы­ваются в одинаковом виде в случае теплопередачи и переноса массы. Кроме того, одни из этих безразмерных величин, на­пример число Стэнтона, представляют собой комбинации дру­гих величин, а некоторые имеют более одного названия.

В качестве примера использования безразмерных величин можно рассмотреть процесс теплопередачи. Когда имеет место только естественная конвекция, теплопередача зависит исклю­чительно от структуры потока, определяемой числом Гразгофа, а число Рейнольдса может быть исключено из безразмерных уравнений, описывающих этот процесс. В условиях же принуди­тельной конвекции эффектами структуры потока обычно мож­но пренебречь и исключить из уравнений число Гразгофа. Сле­довательно, уравнение, использующееся в случае естественной конвекции, имеет вид

 (68), а в случае принудительной конвекции —  (69).

При увеличении масштаба возникают проблемы, связанные с экстраполяцией данных, полученных в лаборатории или на полупроизводственной установке, на случай промышленной уста­новки. Оборудование для биотехнологической промышленности можно успешно создавать и эксплуатировать только при усло­вии правильного масштабирования. Ясно, что с проблемой уве­личения масштаба мы сталкиваемся при конструировании всех установок, используемых в биотехнологических процессах, включая теплообменники, центрифуги, испарители, сушилки и т. д., но здесь мы рассмотрим в основном биореакторы.

Любой материальный объект или физическая система ха­рактеризуются тремя параметрами: размером, формой и со­ставом. Все эти параметры меняются независимо друг от дру­га, так что два объекта могут различаться по размеру, но иметь одинаковую форму и состав или быть одинаковыми только по форме, но существенно различаться по размерам и составу. Принцип подобия устанавливает взаимосвязь между физическими системами разных размеров; на нем основано увеличение или уменьшение масштабов процессов и оборудо­вания. Согласно этому принципу, пространственная и времен­ная конфигурации системы определяются отношением между соответствующими величинами внутри систем и не зависят от того, в каких единицах эти величины измеряются. Принцип подобия нередко путают с методом анализа размерностей, хотя логически они совершенно различны. Первый из них — это об­щий принцип природы, тогда как второй — всего лишь один из методов его реализации.

Биотехнолог имеет дело со сложными системами, включаю­щими твердые тела и жидкости, в которых происходит пеоенос энергии и вещества и протекают различные реакции; для таких систем принцип подобия связан в основном с понятием формы. Когда понятие формы применяется к сложным биотехнологи­ческим системам, оно включает помимо геометрических про­порций и такие факторы, как структура потока жидкости, тем­пературные градиенты, зависимость концентрации от времени и т. д. Системы, обладающие одинаковой конфигурацией πo^, одному или более из этих параметров, можно рассматривать как подобные.

Подобие можно определить двумя способами: устанавливая отношение результатов различных измерений для одного и то­го же объекта, т. е. внутренние пропорции, или отношения меж­ду результатами соответствующих измерений разных объектов, т. е. масштаб. Геометрическое подобие лучше всего определя­ется через масштабные соотношения, а подобие по таким пе­ременным, как скорость, сила или температура, — через внут­ренние соотношения для каждой системы. Эти внутренние со­отношения представляют собой безразмерные величины, харак­теризующие подобие в различных условиях.

Для систем, в которых протекают биотехнологические про­цессы, существуют четыре типа подобия: 1) геометрическое, 2) механическое, 3) тепловое и 4) химическое, причем каждый из этих типов подобия связан со всеми остальными. Для полно­го химического подобия необходимо наличие геометрического, механического и теплового подобия, но часто приходится огра­ничиваться приближенным химическим подобием, например, когда имеет место лишь приближенное механическое подобие?. На самом деле такой элемент приближения имеется всегда, поскольку в реальных системах обязательно существуют возму­щения и идеальное подобие становится недостижимым. Так, рассматривая потоки жидкости в геометрически подобных си­стемах, мы не можем считать их идентичными, поскольку нет гарантии, что все неровности поверхностей геометрически по­добны.

Из рассмотрения четырех типов подобия, перечисленных вы­ше, следует, что геометрическое подобие между двумя объектами имеет место тогда, когда каждой точке одного из них соответ­ствует определенная точка другого. Однако каждой точке пер­вого объекта может соответствовать более одной точки второ­го; кроме того, масштаб может быть одинаковым не по всем •осям. О подобии объектов с такими различиями в масштабе говорят как об искаженном.

Механическое подобие включает подобие статическое, ки­нематическое и динамическое; каждое из них можно рассмат­ривать как распространение понятия геометрического подобия  на стационарные или движущиеся системы, на которые действу­ют силы. Статическое подобие относится прежде всего к де­формации структур и представляет для биотехнологов лишь не­большой интерес. Напротив, кинематическое и динамическое подобие очень важны и касаются систем, для которых харак­терно движение. В случае геометрического подобия использу­ется декартова система координат, при кинематическом подо­бии вводится дополнительная переменная — время. О геомет­рически подобных движущихся системах говорят как о кине­матически подобных в тех случаях, когда соответственные ча­стицы описывают за соответственные интервалы времени по­добные траектории. Когда две геометрически подобные жидкие •системы подобны кинематически, свойства потоков геометри­чески подобны, а процессы переноса массы и тепла в этих двух системах связаны друг с другом простыми соотношениями. Ки­нематическое подобие в жидкостях влечет за собой геометриче­ское подобие как турбулентных систем, так и пограничных (пристеночных) слоев жидкости. Динамически подобны силы (гравитационные, центробежные и т. п.), под действием кото­рых осуществляется ускоренное или замедленное движение тел в динамических системах. В жидких и дисперсионных системах кинематическое подобие предусматривает и динамическое подо­бие, поскольку характер движения в таких системах определя­ется приложенными силами. Динамически подобные системы —- это геометрически подобные движущиеся системы, в которых соотношения между всеми соответственными силами одинако­вы. Динамическое подобие в потоке жидкости очень важно для предсказания изменения давления или потребления энергии; в случае переноса массы и теплопередачи оно имеет только косвенное значение как способ установления кинематического  подобия.

Понятие теплового подобия применяется в случае техноло­гических систем, в которых происходит теплопередача; в этом случае к единицам длины, силы и времени добавляется темпе­ратура. Тепло может передаваться от одной точки системы к другой с помощью разных механизмов: излучения, теплопровод­ности, конвекции или переноса вещества под действием гради­ента давления. Первые три процесса осуществляются за счет  разницы в температурах, а четвертый определяется характе­ром потока в системе. Тепловое подобие имеет место в геомет­рически подобных системах, когда отношения соответственных разностей температур постоянны, а когда такие системы нахо­дятся в движении, они также и кинематически подобны. Теп­ловое подобие должно учитываться при разработке режима сте­рилизации биореакторов, особенно в плане теплового поврежде­ния материала, а также при охлаждении биореакторов.

Понятие химического подобия относится к системам, в кото­рых протекают различные реакции и состав которых меняется от точки к точке либо — в случае периодических или цикличе­ских процессов — во времени. При этом никаких новых фунда­ментальных единиц не вводится, однако должны быть заданы один или более концентрационных параметров в зависимости от числа независимо изменяющихся химических компонентов, no- которым должно быть установлено подобие. Химическое подо­бие имеет место в геометрически подобных системах и систе­мах с тепловым подобием, когда отношение между соответст­венными разностями концентрации остается постоянным и ког­да эти системы, если они находятся в движении, кинематиче­ски подобны. Внутренним критерием, который характеризует химическое подобие, в дополнение к тем критериям, которые- необходимы для кинематического и теплового подобия, яв­ляется отношение скорости образования продукта к скорости всего потока или к скорости молекулярной диффузии.

Механическое, тепловое или химическое подобие между гео­метрически подобными системами определяется такими крите­риями, как соотношения размеров, сил или скоростей внутри этих систем. Поскольку эти критерии представляют собой от­ношение между одинаковыми величинами, они безразмерны и могут быть получены с помощью анализа размерностей.

Безразмерные критерии подобия представляют собой отно­шения физических величин, являющихся функциями или раз­личных движущих сил, или сил сопротивления, которые лими­тируют процесс. В реальных системах часто существуют мно­жественные лимитирующие факторы. Например, сопротивление движению жидкости может быть обусловлено вязкостью, гравитационными силами или силами поверхностного натяже­ния, для которых соответствующими безразмерными величина­ми являются числа Рейнольдса, Фруда и Вебера. Для самого простого случая гомологичных систем с разными абсолютными размерами эти три критерия несовместимы, поскольку для них имеет место разная функциональная зависимость скорости движения жидкости от линейных размеров; так, для одинако­вых чисел Рейнольдса скорость=длине^-1, для одинаковых чисел  Фруда скорость=длине⁰’⁵, для одинаковых чисел Вебера скорость=длине^-0’⁵. При увеличении масштаба сложного биотех­нологического процесса лучше всего было бы найти такие усло­вия, при которых скорость процесса в целом определялась в основном каким-то одним безразмерным критерием, но, как правило, приходится использовать как минимум два критерия.

Для биореакторов с вращающимися мешалками, благодаря которым воздух диспергируется в толще культуральной среды, очень часто основным экономическим фактором при масштаби­ровании является потребление энергии при перемешивании. В общем виде безразмерное уравнение для двухфазного пото­ка жидкости в емкости с вращающейся мешалкой выглядит следующим образом:  (70)  

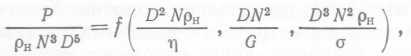или  (71),

где P — потребляемая энергия, р_н— плотность жидкой (не­прерывной) фазы, N — скорость вращения мешалки, D — диа­метр мешалки, η∏ — вязкость жидкой (непрерывной) фазы, G — гравитационная постоянная, σ — поверхностное натяже­ние.

Для систем газ — жидкость зависимость от чисел Ройнольдса и Вебера в уравнении потока жидкости можно с достаточной точностью представить как степенные функции этих чисел, хо­тя показатели степени и не являются постоянными для всех условий. Далее, зависимость от числа Фруда возникает только при наличии вихрей на поверхности жидкости, а в биореакто­рах с вращающимися мешалками образование вихрей предот­вращается с помощью перегородок. Следовательно, для аэри­руемых биореакторов с вращающимися мешалками

Np = ∕(N_βe)^α (N_we)V, (72),

где показатели степени а и у зависят от условий процесса, в частности от структуры потока.

Анализ размерностей массопередачи в аэрируемых геомет­рически подобных биореакторах с мешалками дает  (73)

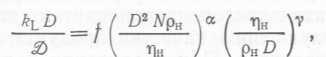или  (74), 

где kL — коэффициент массопередачи, D — коэффициент моле­кулярной диффузии кислорода в жидкой (непрерывной) фазе. Хотя у нас нет оснований сомневаться в применимости уравне­ний (72) и (73) к случаю биореакторов с вращающимися ме­шалками, следует помнить о тех трудностях, которые возника­ют при оценке влияния перемешивания на биологическую ак­тивность; эти трудности вполне могут привести к несостоятель­ности обсуждаемого подхода. Скорость вращения лопастей ме­шалки πND задает максимальную скорость сдвига в аэрируе­мых биореакторах, от которой зависит вероятность поврежде­ния жизнеспособных клеток, особенно нитевидных бактерий или образующих хлопья микробов. При увеличении размеров биотехнологических установок необходимо уделять особое вни­мание связям между механическими и физическими факторами, с одной стороны, и биологическими — с другой. В противном случае задача увеличения масштаба вряд ли будет решена кор­ректно.

• 10.3.3. Перенос кислорода

Одна из основных задач, которые приходится решать химикам-технологам при конструировании биореакторов, — это обеспе­чение эффективного переноса кислорода в промышленных био­реакторах, где осуществляются аэробные микробиологические процессы. Независимо от того, в каком режиме осуществляется аэробный микробиологический процесс — периодическом, полу­непрерывном или непрерывном, — в установку должен непре­рывно подаваться кислород для достижения достаточно высо­кой производительности. Потребность аэробной культуры в кислороде зависит от концентрации микроорганизмов в реакто­ре, скорости их роста и соответствующего коэффициента вы­хода. В некоторых случаях могут играть роль и другие факто­ры, например необходимость удаления из культуры двуокиси углерода, особенно для процессов, в которых в качестве источ­ника кислорода используется воздух, который как раз и слу­жит источником кислорода в подавляющем большинстве аэроб­ных микробиологических процессов. При тех температурах, при которых обычно протекают микробиологические процессы (10—40⁰C), и при атмосферном давлении равновесная концентрация растворенного кислорода крайне мала по сравнению с концент­рациями в растворе почти всех основных питательных веществ или субстратов, хотя именно концентрация последних лимити­рует рост микроорганизмов в непрерывном проточном хемоста- те. Такой недостаток кислорода приводит к снижению произво­дительности, к ухудшению качества продукта или к образова­нию побочных продуктов. При реализации большинства аэроб­ных микробиологических процессов расходы на снабжение  кислородом составляют значительную часть общей стоимости производства.

В равновесии растворимость газа в жидкости представляет собой весьма небольшую, вполне определенную величину, зави­сящую от природы этих газа и жидкости, от температуры  и давления в системе. В случае газовых смесей, например возду­ха, растворимость компонентов зависит от парциального дав­ления каждого из них. При прочих равных условиях, чем выше температура, тем меньше растворимость, и чем выше давле­ние (или парциальное давление), тем растворимость выше. За­висимость между растворимостью газа и давлением известна как закон Генри, согласно которому при постоянной температу­ре масса газа, растворенного в данном объеме жидкости, про­порциональна давлению газа, с которым эта жидкость находит­ся в равновесии. Большинство культуральных сред представля­ют собой разбавленные водные растворы, и для простоты их можно считать сходными с водой. Концентрация кислорода, растворенного в воде, находящейся в равновесии с воздухом, т. е. в состоянии насыщения, при постоянной температуре и по­стоянном суммарном давлении равна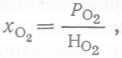 

где po₂ —парциальное давление кислорода в воздухе, Ho₂ — постоянная Генри для данной системы при соответствующей температуре. Значения этих постоянных приводятся в физических и химических справочниках, и нужно только правильно вы­брать единицы измерения.

Для описания переноса (абсорбции) газов в жидкостях обычно используются три гидродинамические модели: 1) мо­дель двух пленок Льюиса — Уитмена; 2) модель проницаемо­сти с систематически обновляемой поверхностью (модель Хиг­би); 3) модель проницаемости со случайно возобновляемой по­верхностью (модель Данквертса).

Для описания физической абсорбции газов системами аэроб­ных микробных культур обычно применяют модель Льюиса —Уитмена, поэтому только ее мы здесь и рассмотрим. Перенос кислорода из жидкой фазы в бактериальную клетку также ча­сто рассматривают с позиций, аналогичных модели двух пле­нок.

Согласно модели Льюиса — Уитмена, на поверхности разде­ла фаз газ — жидкость образуются две тонкие пленки, тесно прилегающие к этой поверхности. Пленки являются в основном неподвижными, а в толще газовой и жидкой фаз происходит турбулентное движение. Абсорбция газа осуществляется в ходе стационарных процессов молекулярной диффузии в этих двух неподвижных пленках. Считается, что на поверхности раздела фаз газ — жидкость мгновенно устанавливается равновесие, а скорость абсорбции определяется относительными скоростями диффузии в пленках. 

                                          Направление транспорта кислорода

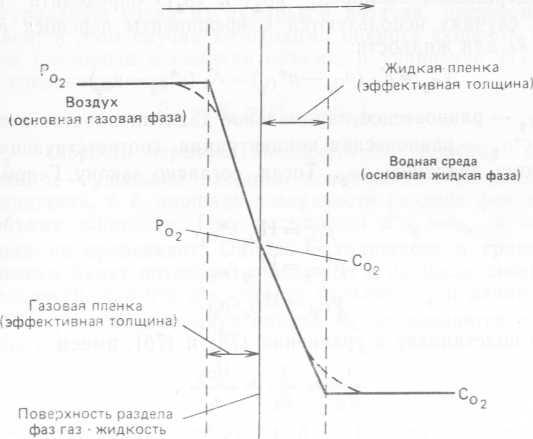
Рис. 10.10. Модель двух (ламинарных) пленок, предложенная Уитменом для процесса физической абсорбции (транспорта) кислорода из воздуха в водную среду (обозначения см. в тексте).

Предположим, что абсорбция осуществля­ется из пузырьков воздуха, диспергированных в жидкости; ра­диус кривизны пузырьков на несколько порядков превышает толщину гипотетической пленки, и транспорт кислорода из пу­зырьков воздуха в жидкость можно представить так, как это сделано на рис. 10.10. В газовой пленке парциальное давление кислорода меняется от po₂ — парциального давления во всем объеме газовой фазы до po₂1 — парциального давления в газо­вой пленке непосредственно у границы раздела фаз; соответст¬венно в жидкой пленке концентрация растворенного кислорода меняется от Co2ι — равновесной концентрации при насыщении, соответствующей po21, до Co2 — концентрации во всем объеме жидкости. Поскольку кислород на поверхности раздела не накапливается, скорость переноса кислорода на единицу площади в газовой и жидкой пленках будет одинакова и равна (76), 

где kG и kL — коэффициенты массопереноса соответственно для газовой и жидкой пленок. Для воздуха и других газовых сме­сей, содержащих кислород, po₂i и Co₂ι определить нельзя; в этих случаях используются коэффициенты переноса Ka для газа и kL для жидкости: фазы kG практически равен коэффициенту для газовой пленки ka;

(77),

где p*o2 — равновесное парциальное давление, соответствующее Co2, a c*o2 —равновесная концентрация, соответствующая парциальному давлению po2∙ Тогда, согласно закону Генри, получаем

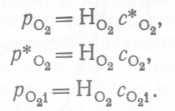(78,79,80)

Сделав подстановку в уравнения (75) и (76), имеем 

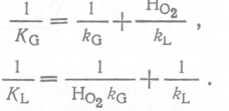 (81,82)

Величины, обратные коэффициентам массопереноса, называются коэффициентами сопротивления транспорту, т. е. 1∕kG и 1∕kL — соответственно коэффициенты сопротивления в газовой и жидкой пленках, a 1/KG И 1/KL— соответственно коэффициенты сопротивления для всего объема газа и всего объема жидкости. Их относительные значения зависят от растворимости газа. При абсорбции очень хороню растворимого газа, например аммиака в воде, постоянная Генри HNH3 очень мала, и последним членом в уравнении, аналогичном (81), можно пренебречь, так что коэффициент массопереноса для газовой абсорбциb лимитируется процессами, происходящими в га­зовой пленке. При абсорбции (транспорте) кислорода, который растворяется в воде слабо, постоянная Ho₂ очень велика, так что в уравнении (82) член 1∕Ho₂⅛g очень мал и им можно пре­небречь. Коэффициент массопереноса для жидкой фазы Kl практически равен коэффициенту массопереноса для жидкой пленки k_L; абсорбция кислорода лимитируется процессами, про­текающими в пленке жидкости. Когда газовая фаза содержит кислород, Po_sI = Po₂ и k_a — бесконечно большая величина, так что абсорбция в этом случае также лимитируется процессами в жидкой пленке.

В большинстве аэробных биореакторов кислород поступает в культуральную среду из пузырьков воздуха, диспергирован­ных в ней; в этом случае необходимо оценить скорость массопередачи кислорода в единице объема, и уравнение (77) при­нимает следующий вид:

 (83),

где Ro₂ — скорость переноса кислорода на единицу объема жидкости, а — удельная площадь поверхности раздела фаз газ — жидкость, т. е. площадь поверхности раздела фаз на еди­ницу объема жидкости. При насыщении c*o₂=Co₂ и перенос кислорода не происходит. Однако находящиеся в среде мик­роорганизмы будут потреблять кислород в процессе своей жиз­недеятельности, так что c*o₂ станет больше Co₂ и начнется пе­ренос. В случае модели двух пленок Kl определяется следую­щим образом:

 (84) , где KL — коэффициент диффузии, δ — толщина пленки жидко­сти.

Для другой модели поглощения газа Kl определяется иным способом. В модели Хигби   (85),

а в модели Данквертса(86).

где t* — это время нахождения элементарного объема жидко­сти на поверхности раздела, a ⅛ — эквивалентное время диф­фузии.

Транспорт кислорода из пузырька в жидкую среду — это лишь часть общего процесса переноса кислорода к бактериальным клеткам. Как было показано для переноса кислорода из  пузырьков в жидкость, транспорту препятствуют разного рода факторы, один из которых является лимитирующим. Понятие сопротивления переносу можно распространить и на последую­щие стадии процесса. Кислород, поступив в культуральную сре­ду, должен затем транспортироваться к месту его использова­ния в микроорганизме. Сопротивление переносу складывается из сопротивления со стороны жидкой фазы, которым для невязких, ньютоновских жидкостей в условиях полной тур­булентности можно пренебречь, из сопротивления со стороны жидкой пленки, прилегающей к поверхности бактериальной клетки, хлопьям, осадку или к поверхности мицелия  либо внутриклеточного сопротивления в случае дисперсионных культур, либо межклеточного (включая и внутриклеточное) в- случае хлопьев, осадков и мицелия. 

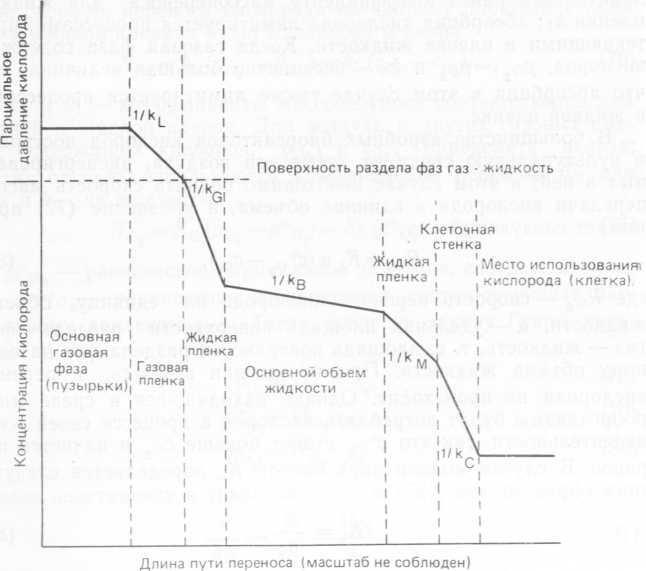
Рис. 10.11. Различные типы сопротивления транспорту кислорода из пузырька газа к месту его использования микроорганизмом (обобщение модели Уитме­на; обозначения см. в тексте).

Все типы сопротив­ления переносу кислорода представлены на рис. 10.11. В слу­чае дисперсионных культур перенос кислорода лимитируется сопротивлением в жидкой пленке пузырька. Когда же микроорганизмы растут в виде хлопьев, осадков или мицели­альной массы, в некоторых случаях роль лимитирующего фак­тора играет не сопротивление в жидкой пленке газового пузырь­ка, а внутримежклеточное сопротивление или сопротивление конгломерата.

В связи с очевидностью роли переноса кислорода из пузырь­ков газа в жидкость попытаемся с помощью уравнения (83) оценить возможности увеличения скорости транспорта кисло­рода. В принципе можно варьировать все три члена этого урав­нения: K_l, а и (c*o_j-Co₂) (последний член характеризует дви­жущую силу процесса). Однако Kl является характеристикой системы в целом и не может изменяться независимо, поэтому обычно ее считают константой, хотя под действием поверхност­но-активных веществ, присутствующих в микробиологических установках, она все-таки изменяется. Удельную площадь по­верхности раздела фаз газ — жидкость и член, характеризую­щий движущую силу, легко увеличить, изменяя контролируе­мым образом условия проведения процесса. Обычно первая из этих величин возрастает при интенсификации перемешива­ния, а вторая — при увеличении суммарного или парциального давления.

Удельная площадь поверхности раздела фаз газ — жид­кость определяется следующим образом:  (87),

где ε — задержка газа на единицу диспергируемого объема, U — средний диаметр пузырьков (в случае пузырьков неодина­кового размера). Обычно для определения среднего диаметра пузырька используют формулу Саутера:

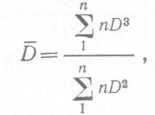 (88), 

где п — число пузырьков, D — диаметр эквивалентной сферы. Ясно, что для интенсификации транспорта кислорода путем увеличения а необходимо либо повысить содержание газа в .диспергируемой среде (т. е. ε), либо уменьшить средний диа­метр пузырьков.

Диспергирование пузырьков газов в жидкостях — сложный процесс. Независимо от способа получения пузырьков для нихвсегда наблюдается некое распределение по размерам. Размер любого диспергированного пузырька определяется равновесием между двумя основными типами напряжений: напряжением сдвига и поверхностным натяжением. На размер пузырьков заметно влияет присутствие в среде растворенных неорганических и органических веществ, при этом изменяется либо коалесценция, либо поверхностное натяжение.

В биореакторах коалесценция и поверхностное натяжение не могут изменяться независимо друг от друга и произвольным образом, однако несомненно они изменяются в ходе процесса или в результате добавления соединений, контролирующих ценообразование. Теоретически уменьшение среднего размера пузырьков при диспергировании газов в жидкостях может происходить при интенсификации перемешивания. Однако на самом деле при обычных удельных мощностях перемешивания средний размер пузырьков остается примерно постоянным, зато заметно увеличивается содержание газа, т. е. другой компонент величины а; это связано с рециркуляцией жидкости, благодаря которой в свою очередь снижается потеря пузырьков газа. Механизм разрушения пузырьков в изотопическом турбулент¬ном потоке мы обсуждать не будем. Отметим лишь, что в результате рассмотрения этих механизмов для случая отсутствия коалесценции было получено уравнение, удовлетворяющее множеству имеющихся экспериментальных данных для систем с очень высокой энергоемкостью: 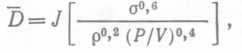 (89), где J — константа, σ — поверхностное натяжение, р — плотность жидкости, P/V — энергоемкость на единицу объема в условиях насыщения газом. При наличии коалесценции уравнение (89) принимает вид  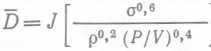  (90),

Здесь показатель степени а, в который возводится величина ε, характеризует степень коалесценции.
Итак, очевидно, что задержка газа и средний размер пузырьков прямо связаны между собой; при этом задержка газа зависит от интенсивности перемешивания и от объемной скорости потока газа. Соответствующее эмпирическое уравнение для жидкости с постоянными реологическими характеристиками имеет вид: 

 (91), где J', β и γ — константы, зависящие от системы и оборудования, a V_n — поверхностная скорость газа, т. е. отношение объ­емной скорости газового потока к площади поперечного сечения биореактора. В биореакторах с вращающимися мешалками и высокой энергоемкостью происходит рециркуляция значитель­ной части газовой фазы и соответственно уменьшается влияние поверхностной скорости газа на величину ε. В то же время в барботажных биореакторах относительная роль V_n сильно воз­растает.

Оценивая транспорт кислорода из газовой фазы в жид­кость в микробиологических реакторах, Эндрью (Andrew, 1982) высказал мнение, что при конструировании любых промышлен­ных аэробных биореакторов, в том числе больших тэнков с ме­шалками, их можно рассматривать как аппараты колонного типа со свободным прохождением пузырьков газа по высоте аппарата. Крупные биореакторы-тэнки с мешалками относят к категории вышеупомянутых биореакторов, основываясь на яв­лении массопереноса, а также в связи с тем, что при обычной промышленной энергоемкости мешалка не способна создавать, рециркуляцию жидкости, достаточную для возврата пузырьков, стремящихся выйти на поверхность жидкости.

Рассмотрим теперь вопрос о возможности изменения скоро­сти транспорта кислорода путем изменения того члена уравне­ния (83), который характеризует движущую силу процесса, т. е. (c*o₂—^co₂). Здесь имеется несколько возможностей. В первую очередь уменьшение до минимума рабочей концент­рации растворенного кислорода в среде, т. е. Co₂. Однако, ког­да эта величина приближается к нулю, дальнейшее увеличение Движущей силы становится невозможным. Максимально дости­жимая, постоянная скорость транспорта кислорода До₂.ш равна  (92).

Уменьшать содержание растворенного кислорода в культураль­ной среде следует с осторожностью, поскольку микроорганиз­мы при этом вынуждены будут расти в условиях недостатка кислорода, что может отрицательно сказаться на их росте и/или образовании продукта. Если микроорганизмы растут в виде хлопьев, образуют осадок или мицелий и величина l∕⅛_c стано­вится фактором, лимитирующим весь процесс транспорта кис­лорода, концентрация Co₂ должна поддерживаться на уровне значительно выше нуля, если мы хотим, чтобы во всем объеме микробной биомассы, находящейся в реакторе, поддерживался аэробный метаболизм.

Прежде чем говорить об изменении c*o₂, следует сначала определить, какое именно парциальное давление кислорода со­ответствует c*o₂ в тех или иных типах биореакторов. Для био­реакторов с высокой интенсивностью перемешивания, т. е. ре­акторов, которые обычно используются в лаборатории, было показано, что газовая и жидкая фазы полностью перемешива­ются. Следовательно, парциальное давление кислорода в дис­пергированных пузырьках равно парциальному давлению кис­лорода в газе, выходящем из жидкости, т. е. в свободном про­странстве биореактора. Для биореакторов колонного типа со свободным прохождением пузырьков по высоте биореактора, в том числе и для промышленных биореакторов с перемешивани­ем, работающих в условиях обычной энергоемкости, в первом приближении можно считать, что жидкая фаза перемешивает­ся полностью, а газовая находится в режиме идеального вытес­нения, т. е. существует градиент парциального давления кисло­рода в направлении от дна биореактора к его верху. Для этих двух крайних случаев уравнение (83) можно переписать сле­дующим образом:

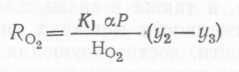 (93) 

(для случая полного перемешивания) и

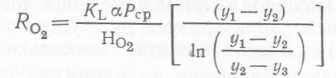 (94)

(для случая полного вытеснения). Здесь P — давление в сво­бодном пространстве, P_cp — среднее рабочее давление в реакто­ре (давление в рабочем пространстве+гидростатическое давле­ние) z∕ι, ι∕2 и уз — мольные доли кислорода во входящем и вы­ходящем газе и в газовой смеси, соответствующей равновесной концентрации растворенного кислорода.

Из уравнений (93) и (94) с очевидностью следует, что с увеличением давления в свободном пространстве биореактора повышается скорость транспорта кислорода в обоих рассмот­ренных случаях, а с увеличением парциального давления кис­лорода путем обогащения им газовой смеси, продуваемой че­рез биореактор, или полной замены ее кислородом повышается скорость транспорта кислорода в случае полного вытеснения. В реакторах с идеальным перемешиванием парциальное давле­ние кислорода в пузырьках, а следовательно, и скорость транс­порта кислорода должны увеличиваться с уменьшением кон- .версии кислорода; однако это вряд ли можно считать экономи­чески целесообразным.

Поскольку микроорганизмы имеют тенденцию скапливаться у поверхности раздела между воздухом и жидкостью, видимо, правильнее было бы записать уравнение (82) следующим обра­зом:

 (95).

Ясно, что в отсутствие такого накопления £'=1, однако обычно, особенно в случае бактерий значительно меньшего размера,, чем толщина пленки (~20 мкм), концентрация их у поверхно­сти раздела фаз будет гораздо больше, чем в толще жидкости. Влияние этого явления на транспорт кислорода, вероятно, в; какой-то степени сходно с эффектами, наблюдаемыми при по­глощении газа в условиях одновременного протекания химиче­ской реакции; тем не менее прямая аналогия здесь вряд ли воз­можна, поскольку концентрация бактерий внутри пленки меня­ется нелинейно, а текучесть пленки уменьшается из-за присут­ствия в ней бактериальных клеток.

• 10.3.4. Теплопередача и охлаждение'биореактора

К числу наименее разработанных проблем биотехнологии отно­сятся разнообразные проблемы осуществления процессов тепло­передачи, которые обеспечивают поддержание температуры аэрируемой культуральной среды на уровне, соответствующем оптимуму анаболической и катаболической активности данных микроорганизмов. Для большинства из них диапазон темпера­тур, оптимальных для роста или образования продукта, очень- узок, нередко всего несколько градусов. При температурах ни­же оптимальной скорость роста любого микроорганизма повы­шается в ответ на повышение температуры относительно мед­ленно, а при температурах, лишь, на несколько градусов превы­шающих этот оптимум, происходит резкое снижение скорости роста до нуля. Подавляющее большинство микроорганизмов,, используемых в биотехнологических процессах, — мезофилы: температурный оптимум для них лежит между 15 и 40 °C. Тем­пературный оптимум термофильных микроорганизмов значи­тельно превышает 40^oC, а у облигатных психрофильных микро­организмов он лежит ниже IO⁰C.

При производстве любого валового микробиологического продукта аэробным способом охлаждение биореактора предс­тавляет собой серьезную технологическую проблему. Если тем­пературный оптимум, при котором достигается максимальный выход продукта и производительность, лежит ниже 40 ⁰C, на; охлаждение приходится основная часть производственных расхо­дов. Обычно в практике биотехнологических процессов промыш­ленного масштаба используют в качестве охлаждающей среды воду, а не какой-либо хладагент. При определении размеров охлаждающей поверхности, необходимой для поддержания температуры любого процесса, особое значение имеет макси­мальная температура охлаждающей воды, а производственные расходы на системы охлаждения определяются средней темпе­ратурой охлаждающей воды, используемой на разных этапах процесса. Следует подчеркнуть, что при очистке валового про­дукта требуется значительно меньшее охлаждение, чем при осуществлении обычных биологических процессов. Однако не­которые из недавно разработанных физических методов разде­ления протекают при температурах, близких к обычным, и представляются весьма перспективными в плане использования их в биотехнологии.

Температура охлаждающей воды зависит от многих факто­ров. К ним относятся происхождение этой воды, климатические условия и различия в местоположении установки, а также тип используемой системы охлаждения: это может быть проточная система или система с рециркуляцией. В будущем для охлаж­дения, вероятно, все больше будут применяться замкнутые си­стемы (с рециркуляцией), с тем чтобы исключить тепловое и возможное химическое загрязнение окружающей среды в ре­зультате сброса воды из проточных систем охлаждения. В ус­ловиях умеренного климата и при использовании мезофильных организмов в крупных, интегрированных производствах опти­мальная температура процесса будет лишь немного отличаться от температуры охлаждающей воды.

Хотя калориметрические методы измерения количества теп­ла, выделяющегося при росте и дыхании микроорганизмов, разработаны уже давно, использованию этого процесса посвя­щено сравнительно немного работ. Измерения количества выде­ляющегося тепла производили обычно для оценки интенсивно­сти роста микроорганизмов. В аэробных микробиологических процессах количество тепла, выделяющегося в единицу време­ни, прямо пропорционально скорости потребления кислорода, которая в свою очередь связана с ростом с помощью соответст­вующего коэффициента выхода. Считается, что это эмпириче­ское соотношение между скоростью потребления кислорода и количеством .выделяющегося тепла можно применять для оцен­ки последней величины, и прямые ее измерения проводят толь­ко в редких случаях. Это соотношение имеет вид

 (96).

Здесь Q — количество тепла, выделяющегося при росте аэроб- щых микробов в единицу времени на единицу объема, Ro₂ — скорость потребления кислорода на единицу объема (равная «скорости транспорта кислорода), k—константа, равная 124, «если Q выражено в ккал• м~³-ч^-1., a Ro ₂—в моль-m~³∙4^¹. Оценки, получаемые с помощью этого уравнения, близки к таковым при расчете количества тепла исходя из теплоты сжигания суб­стратов и микробной биомассы соответствующего состава.

Большинство промышленных биореакторов снабжено ох­лаждающим кожухом и/или внутренними охлаждающими змеевиками. В последнее время для интенсификации процессов в биореакторах как обычной конструкции, так и новых конфи­гураций стали использовать наружные охлаждающие контуры. В некоторых реакторах новых конфигураций внутренняя ох­лаждающая система настолько нарушает основные гидродина­мические рабочие характеристики, что исключает такое охлаж­дение. При увеличении размера реактора создание необходимой внутренней охлаждающей поверхности становится все более трудной задачей. Для геометрически подобных емкостей увели­чение объема пропорционально кубу линейных размеров, при этом площадь увеличивается только пропорционально квадра­ту линейных размеров. Эффективность охлаждения аэробных биореакторов зависит от следующих факторов: 1) переноса тепла от отдельных клеток в культуральную среду; 2) перено­са тепла от культуральной среды, содержащей диспергирован­ные пузырьки газа и микроорганизмы, к охлаждающим по­верхностям; 3) поступления тепла за счет рассеяния механиче­ской энергии, затрачиваемой на перемешивание среды с целью ее аэрации; 4) охлаждения при испарении, выравнивания тем­ператур и работы при расширении, связанной с прохождением воздуха через среду; 5) изменения коэффициента теплопереда­чи вследствие загрязнения охлаждающих поверхностей накап­ливающимися на них микроорганизмами. Потенциальную зна­чимость этих факторов необходимо рассматривать отдельно для каждой технологической системы.

Когда микроорганизмы диспергированы в толще водной сре­ды, как бывает обычно в процессах, где культивируют бакте­рии и дрожжи, скорость теплопередачи лимитируется перено­сом тепла от культуральной среды к охлаждающим поверхно­стям.

Содержимое аэробного биореактора, работающего в услови­ях интенсивного перемешивания, можно представить как массу пузырьков, но нужно еще учесть, что жидкая фаза содержит суспендированные микроорганизмы, оказывающие влияние на ее вязкость. Эта последняя зависит от размера микроорганиз­ма, его морфологии и концентрации, а также от способности синтезировать внеклеточные полимерные продукты.

Одна из основных задач аэрации содержимого биореакто­ра — это получение мелких пузырьков газа и тем самым мак­симальное увеличение площади поверхности, через которую происходит перенос газа в среду. Во многом благодаря свойствам культуральной среды образующиеся в ней пузырьки имеют сферическую форму и относительно слабо деформируются. Фак­тически они представляют собой упругие сферы, гидродинами­ческие свойства которых сходны со свойствами твердых сфери­ческих частиц. Хотя плотность и теплопроводность твердых ча­стиц, с одной стороны, и пузырьков — с другой, явно различны,, поведение пузырьков в некоторых аспектах сходно с поведени­ем частиц в псевдоожиженном слое, хотя в последнем случае- содержание диспергированных частиц обычно выше.

Плотность клеток микроорганизмов очень близка к плотно­сти водной среды, в которой они растут, и при анализе тепло­передачи в дисперсионных культурах бактерий и дрожжей, обычно имеющих диаметр эквивалентной сферы меньше 10 мкм, культуральную среду можно рассматривать как одно­родную водную фазу. В аэрируемых биореакторах перенос теп­ла от культуральной среды к охлаждающим поверхностям осу­ществляется путем принудительной конвекции. Чтобы судить о потенциальной эффективности охлаждения, необходимо оце­нить соответствие характеристик водно-газовых смесей, образу­ющихся при оптимальном транспорте кислорода, факторам, способствующим увеличению теплопередачи от этой смеси к поверхности.

Благодаря хорошим характеристикам теплопередачи реак­торы с псевдоожиженным слоем применяются для проведения реакций, которые требуют тщательного контроля температуры. Из-за ожижения частиц увеличивается коэффициент теплопере­дачи между образуемым ими слоем и теплопередающими по­верхностями. Это увеличение определяется в основном тремя факторами: 1) высокой теплоемкостью на единицу объема ча­стиц, благодаря чему они выполняют функцию теплоперенося­щих агентов; 2) разрушением частицами ламинарного слоя на теплопередающей поверхности и вследствие этого уменьшением эффективной толщины этого слоя; 3) нестационарностью про­цесса теплопередачи, обусловленной тем, что частицы движут­ся к теплопередающей поверхности и от нее в виде «пакетов».

Проанализируем значимость этих факторов в применении к процессу диспергирования газа в жидкости. Если главную роль играет первый фактор, то коэффициент теплопередачи между пузырьками и теплопередающей поверхностью будет существенно меньше из-за низкой теплоемкости пузырьков. Ес­ли основным является второй фактор, то коэффициент тепло­передачи будет больше, а если третий, то может наблюдаться повышенная коалесценция и образование сгустков. В псевдо­ожиженных системах задержка твердых частиц нередко дости­гает 0,4, тогда как в реакторах с обычным потреблением энергии задержка газа вряд ли превышает 0,12. При задержке вы­ше 0,2 начинается образование газовых «пробок».

В барботажных колоннах пробулькивание газа через жид­кость приводит к двум типам перемещений: 1) циркуляции всего содержимого, вызываемой всей массой пузырьков; 2) ло­кальным микроперемещениям, вызываемым отдельными пу­зырьками. Экспериментальные данные для суммарного коэффициента теплопередачи в условиях охлаждения жидкости, в которой диспергированы пузырьки газа, за счет теплопередачи к стенке колонны описываются уравнением  (97),

а за счет теплопередачи к охлаждающему змеевику — уравне­нием

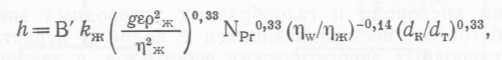 (98),

где h — суммарный коэффициент теплопередачи, В и В' — кон­станты для системы, kж — теплопроводность жидкости, g — гра­витационная постоянная, ε — задержка газа, р_ж — плотность жидкости, η>_κ — вязкость жидкости, Np_r — число Прандтля, η_w — вязкость жидкости при температуре теплопередающей  поверхности, d_κ — диаметр колонны, d_τ — диаметр трубки ох­лаждающего змеевика. Ни одно из этих уравнений нельзя пря­мо использовать в случае биореактора с интенсивным переме­шиванием с помощью мешалки. Из-за значительной рецирку­ляции в реакторах подобного типа показатели степеней этих уравнений должны быть другими.

Для интенсификации переноса кислорода в биореакторах системы аэрации должны обеспечивать образование как можно более мелких пузырьков. Однако при уменьшении размера пу­зырьков уменьшается теплопередача. C другой стороны, тепло­передача увеличивается при увеличении задержки газа. Из этого следует, что в биореакторах с высокой скоростью перено­са кислорода будет, при прочих равных условиях, наблюдаться и более интенсивная теплопередача.

• 10.3.5.   Конверсия и рециркуляция

Как мы уже говорили, основным технологическим фактором, от которого зависит экономичность любого микробиологическо­го процесса, является производительность биореактора. Одна­ко в случае нерастворимых или несмешивающихся с водой суб­стратов и нелимитирующих рост питательных веществ сущест­венную роль начинает играть и величина конверсии. Удельную конверсию субстрата или какого-либо питательного вещества можно определить как отношение массы использованного суб­страта к массе субстрата, исходно введенного в систему. Для микробиологических процессов удельная конверсия полностью растворимого, лимитирующего рост субстрата практически рав­на единице, т. е. остаточная концентрация субстрата, завися­щая от сродства участвующих в процессе микроорганизмов к лимитирующему субстрату, близка к нулю. Для нерастворимых или несмешивающихся с водой субстратов и для нелимитирую­щих рост питательных веществ удельная конверсия часто быва­ет значительно меньше единицы. Для таких систем коэффици­ент конверсии, определяемый как вес сухой микробной био­массы или продукта, получаемых на единицу веса введенного субстрата или питательного вещества, будет меньше соответст­вующего коэффициента выхода. В одних случаях величина конверсии кислорода и газообразных углеродных энергетиче­ских субстратов, несмешивающихся с водой и нерастворимых в ней углеродных энергетических субстратов, а также раство­римых нелимитирующих рост питательных веществ определя­ется режимом работы биореактора, в других более важными факторами являются массоперенос, геометрия биореактора и технологические параметры.

Хотя стоимость сырья при аэробной переработке и не повы­шается из-за использования воздуха в качестве источника кис­лорода, капитальные и эксплуатационные расходы значительно возрастают в связи с необходимостью получения сжатого воз­духа и его стерилизации. В процессах промышленного масшта­ба важно снизить такие расходы до минимума, максимально увеличивая степень конверсии кислорода, при условии, что рас­ходы на это не приведут к снижению экономичности процесса в целом.

Если в качестве источника кислорода используется воздух, то удельная конверсия кислорода в высокоэффективных лабо­раторных биореакторах редко превышает 0,2, а в обычных про­мышленных биореакторах она обычно составляет ~0,1. Даже при таких низких величинах конверсии кислород нередко явля­ется лимитирующим рост фактором, поскольку скорость его транспорта не соответствует скорости потребления. Из рассмот­рения уравнения (83), описывающего физическую абсорбцию кислорода культуральной средой, следует, что в системах с пол­ностью перемешиваемой газовой фазой высокие значения удельной конверсии кислорода несовместимы с увеличением скорости транспорта кислорода до максимума. Очевидно, при решении этой проблемы следует учитывать технические и эко­номические факторы. Что касается биореакторов, в которых га­зовая фаза перемещается в режиме полного вытеснения, то по сравнению с полностью перемешиваемыми системами для них следует ожидать значительно более высоких величин конвер­сии кислорода при данной скорости транспорта.

Для увеличения удельной конверсии в технологических си­стемах чаще всего используют рециркуляцию. В случае мик­робиологических процессов такой подход применим в равной мере и к газовой, и к жидкой фазам, впрочем, с некоторыми модификациями.

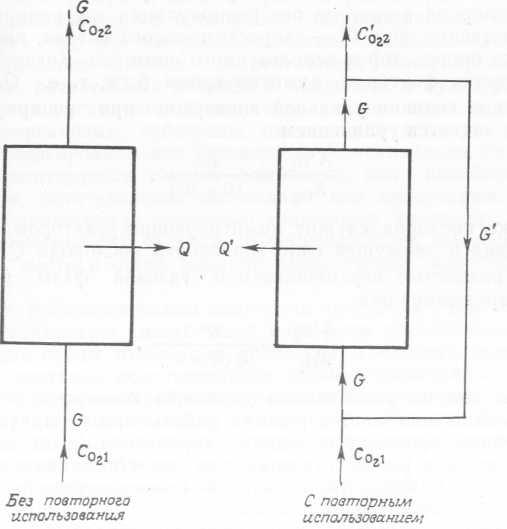
В случае повторного использования газовой фазы их можно рассмотреть на примере двух схем потоков, приведенных на рис. 10.12, — работы в однократном проточном режиме и при рециркуляции газовой фазы в предположении, что переносимый компонент газовой фазы (например, кислород воздуха) является минорным и поэтому газовые потоки, нап­равленные внутрь биореактора и из него, практически одинако­вы. Без рециркуляции удельная конверсия кислорода в возду­хе Хо„ может быть представлена в виде 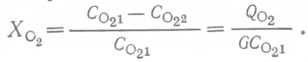 (99)

В условиях рециркуляции соответствующая величина X'o равна

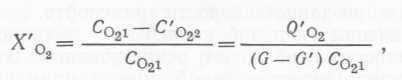 (100)

где Co₂₁ —концентрация кислорода в потоке газа, поступающе­го в обе системы, Co₂₂ и C'o₂₂ — концентрации кислорода в потоке газа, выходящем из систем без рециркуляции и с ре­циркуляцией соответственно, Qo₂ и Q^,o₂ — скорости утилиза­ции кислорода в системе без рециркуляции и с рециркуляцией соответственно, GhG' — скорости газового потока, проходяще­го через биореактор и используемого повторно. Когда кислород не является фактором, лимитирующим рост, т. е. Qo₂ = Q'o₂, отношение величин удельной конверсии при рециркуляции и без нее задается уравнением

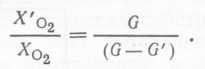 (101),

Если же кислород служит лимитирующим фактором, то из-за изменения в движущей силе транспорта кислорода Qo₂>Q'o₂, и для полностью перемешиваемой газовой фазы уравнение (101) принимает вид

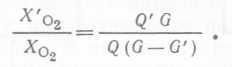 (102).

Как бы мы ни увеличивали удельную конверсию кислорода, при условии постоянства режима работы при рециркуляции га­зовой фазы производительность биореактора будет неизбежно уменьшаться в результате снижения движущей силы транспор­та кислорода. Ясно, что конверсию нельзя оптимизировать не­зависимо от производительности.

Когда в биореакторы добавляют газообразные или летучие углеродные энергетические субстраты, конверсия рассматрива­ется с совершенно иных позиций. В отличие от кислорода воз­духа подобные субстраты представляют собой дорогостоящее сырье, и процессы, в которых они используются, должны быть направлены на достижение очень высокой конверсии либо на полное их использование в системах безотходной технологии с привлечением других процессов. По-видимому, из газообраз­ных углеродных энергетических субстратов наиболее известен метан, хотя в качестве промышленных субстратов можно ис­пользовать и другие газообразные алканы. При условии, что метан как сырье для микробиологических процессов можно использовать непосредственно в виде природного газа и вер­нуть стоимость неутилизованного метана, используя его в та­ких энергоемких процессах, как сушка, в биореакторе могут быть достигнуты относительно высокие значения удельной кон­версии — 0,7—0,8. При этом необходимы реакторы с полным вытеснением газовой фазы и высоким давлением, а также, воз­можно, с повторным использованием газовой фазы. В качестве альтернативы можно использовать несколько последователь­ных реакторов высокого давления с полным перемешиванием.

Обратимся теперь к жидкой фазе и рассмотрим потенци­альные возможности ее повторного использования. Следует подчеркнуть, что все микробиологические процессы протекают при относительно низких концентрациях микроорганизмов, субстратов, питательных веществ и продуктов в культуральной среде. В них расходуется большое количество воды, в которой эти микроорганизмы, субстраты, питательные вещества и про­дукты диспергированы или растворены. Концентрация микробов обычно лимитируется такими факторами, как ингибирование субстратом, питательными веществами или продуктами, а в аэробных процессах — скоростью транспорта кислорода. Одна­ко в технологических системах с рециркуляцией биомассы мо­гут иметь место и очень высокие концентрации микроорганиз­мов.

При микробиологическом получении продуктов с высокой или средней стоимостью имеет смысл повторное использование или регенерация среды только для процессов, в которых задейство­вано уже частично использованное очень дорогостоящее сырье. В случае крупномасштабного производства повторное исполь­зование среды очень выгодно как в плане экономии большого количества высококачественной воды и питательных веществ, так и уменьшения объема сточных вод.

В любой технологической схеме рециркуляции воды/среды ключевым моментом является установление механизма взаимо­действия между различными элементарными операциями, обра­зующими данный цикл. При повторном использовании среды возникают следующие проблемы: 1) накопление в среде инги­биторов из-за метаболической активности, сопровождающейся образованием побочных продуктов, или за счет лизиса в про­цессе рециркуляции; 2) накопление ингибиторов за счет мета­болической активности, лизиса или разрушения клеток в био­реакторе; 3) накопление в сырье нежелательных, неиспользуе­мых примесей; 4) рециркуляция неиспользованных субстратов или питательных веществ, вызывающих нарушение физическо­го и химического равновесия и динамическую неустойчивость в биореакторе.

В случае смешанных культур рециркуляция может приво­дить к избирательному возвращению в биореактор микроорга­низмов, составляющих эту смешанную культуру, с неизбежным нарушением популяционного равновесия в биореакторе.

Повторное использование микробной биомассы — это ско­рее способ интенсификации микробиологических процессов, чем средство увеличения конверсии. В отличие от немногих приме­ров повторного использования газовой или жидкой фазы в промышленных микробиологических процессах повторное ис­пользование микробной биомассы представляет собой хорошо разработанную процедуру, применяемую уже около 70 лет при очистке сточных вод с помощью активного ила.

В математическом представлении непрерывный микробио­логический процесс с повторным использованием микроорганиз­мов эквивалентен непрерывному микробиологическому процес­су, в котором происходит преднамеренная или случайная за­держка микробов в реакторе. Возможно, такая операция най­дет широкое применение в промышленности. Повторное исполь­зование и задержка микроорганизмов дают существенное пре­имущество в тех случаях, когда участвующие в процессе мик­роорганизмы медленно растут или синтезируют не связанный с ростом продукт. Отметим, что при использовании такого спосо­ба интенсификации процесса производительность реактора нельзя будет повысить до тех пор, пока его характеристики, от­носящиеся к теплопередаче и массопереносу, не будут соответ­ствовать рассчитываемому повышению производительности. Если теплопередача или массоперенос в биореакторе в рабочем режиме без рециркуляции или задержки микробов являются лимитирующими факторами, то производительность реактора можно повысить, только улучшив тем или иным способом эти параметры.

• 10.3.6. Характеристики микробных и мицелиальных суспензий

Состав микробов обычно выражают в виде процентного содер­жания углерода, водорода, кислорода, азота и золы в расчете на сухую массу. На самом деле жизнеспособные микроорганиз­мы состоят в основном из воды: на ее долю приходится при­мерно 70% массы клеток.

Форма и размеры разных микроорганизмов описаны в так­сономической литературе, однако следует помнить, что они мо­гут изменяться в зависимости от условий культивирования. При анализе массопереноса и теплопередачи в биореакторах, а так­же процессов отделения микроорганизмов от конечного продук­та часто пользуются понятием «эквивалентный размер» («диа­метр эквивалентной сферы»). Этот термин применяется для
культур, в которых клетки растут в виде дискретно дисперги­рованных суспензий. Понятие эквивалентного размера является полезным упрощением, позволяющим в более простой форме описывать динамическое поведение клеток в суспензии. Кроме того, следует принимать во внимание и плотность суспензии. Обычно она составляет 1,07—1,09 г-см³, хотя иногда бывает и ниже—1,03 г∙cм³. Таким образом, плотность водных куль­туральных жидкостей обычно несколько выше, чем плотность воды.

Единственный случай, для которого было получено выраже­ние для силы сопротивления движению сферических частиц в жидкости, — это погружение частицы с малой скоростью в жид­кость бесконечного объема. Для такой частицы Стокс получил уравнение

 (103), 

где F — сила сопротивления, η — вязкость жидкости, d — диаметр сферической частицы, и — скорость жидкости относи­тельно частицы. На самом деле условия, в которых выполняет­ся закон Стокса, реализуются редко. В большинстве систем ча­стицы непрерывно испытывают ускорение или замедление; кро­ме того, даже в условиях ламинарного потока частицы редко бывают изолированы друг от друга, обычно они взаимодейству­ют между собой.

Конечную скорость погружения частицы и₀ можно полу­чить, приравняв силу сопротивления к эффективной силе тяже­сти, т. е.

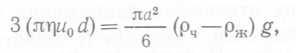(104)

где р_ч и рж — соответственно плотности частицы и жидкости. Отсюда

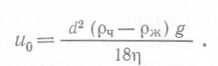 (105).

Закон Стокса для скорости оседания и_с суспензий мелких ча­стиц одинакового размера имеет  вид

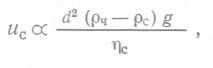 (106)

где рс — средняя плотность суспензии, η_c — кажущаяся вяз­кость. Это уравнение учитывает влияние концентрации частиц как на вязкость, так и на плотность жидкости. В случае неод­нородных частиц в уравнение (106) можно ввести член, учиты­вающий изменение их формы и размера.

Что касается биологических процессов, то для них наибо­лее важным параметром является вязкость соответствующих жидкостей. Она определяется как мера внутреннего трения в жидкости, и в условиях ламинарного потока, т. е. потока с низ­кими числами Рейнольдса, равна отношению напряжения сдви­га к соответствующей скорости сдвига,

т. е.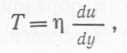 (107), где T — напряжение сдвига, η — вязкость жидкости, du∣dy — скорость сдвига, выраженная через градиент скорости в жид­кости.

Вязкость можно представить либо как произведение силы на время и на величину, обратную квадрату длины, либо как произведение массы на величины, обратные времени и длине. Во всех системах единиц численные значения абсолютной вяз­кости одинаковы. В технической литературе нередко использу­ется термин «кинематическая вязкость», которая представляет собой произведение абсолютной вязкости на величину, обрат­ную плотности жидкости.

Любую жидкость, вязкость которой при постоянных давле­нии и температуре постоянна и не зависит от скорости сдвига, называют ньютоновской. Свойствами ньютоновской жидкости обладают все газы и многие гомогенные жидкости. Однако большинство жидкостей не являются гомогенными; так, у мно­гих культуральных жидкостей вязкость меняется с изменени­ем скорости сдвига. Подобные жидкости называют неньюто­новскими. Для них отношение напряжения сдвига к скорости сдвига равно кажущейся вязкости, которая, разумеется, зави­сит от скорости сдвига. Неньютоновские жидкости можно клас­сифицировать по форме соотношения между напряжением сдви­га и скоростью сдвига.

Очень многие культуральные среды для выращивания бак­терий и дрожжей по существу являются ньютоновскими жидко­стями даже при очень высокой плотности клеток, если только в среду не экскретируются в значительном количестве синтези­руемые этими микроорганизмами биополимеры. Напротив, культуральные жидкости, в которых растут плесневые грибы или актиномицеты, часто являются неньютоновскими, причем степень отклонения их от поведения ньютоновских жидкостей зависит как от концентрации мицелия, так и от его морфоло­гии. При удалении мицелия из большинства культуральных жидкостей плесневых грибов и актиномицетов они становятся ньютоновскими.

Многие культуральные среды для выращивания плесневых грибов и актиномицетов ведут себя как псевдопластические жидкости, т. е. с увеличением скорости сдвига их кажущаяся вязкость сначала уменьшается. График зависимости напряжения сдвига от скорости сдвига для псевдопластической жидкости сначала имеет форму выпуклой кривой, а затем становится линейным. При экстраполяции линейного участка до пересечения с осью напряжений сдвига мы получим точку, отвечающую предельному напряжению сдвига. Для пластических жидкостей предельное напряжение сдвига соответствует предельной точке.

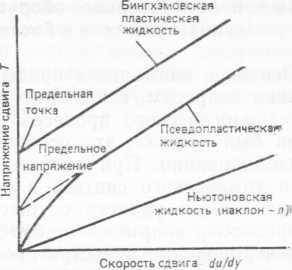
Рис. 10.13. Связь между напряжением сдвига и скоростью сдвига для жидкостей с разными реологическими свойствами.

На рис. 10.13 приведены типы зависимостей между напряжением сдвига и скоростью сдвига. Иногда мицелиальные культуральные жидкости оказы¬ваются тиксотропными, т. е. кажущаяся вязкость уменьшается не только с увеличением скорости сдвига, но и по мере переме¬шивания при данной скорости сдвига.
В общем виде зависимость между напряжением сдвига и скоростью сдвига для неньютоновских жидкостей имеет вид

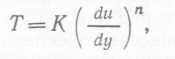 (108), где К и п — константы.

Псевдопластическую жидкость можно в первом приближении охарактеризовать величиной предельного напряжения сдвига и пластической вязкости, т. е. наклоном прямолинейного участка зависимости между напряжением сдвига и скоростью сдвига в линейных координатах. Однако, если построить зависимость напряжения сдвига от скорости сдвига в логарифмических координатах, то линейный участок с наклоном п и точка пересечения К будут определяться начальным участком графика. В истинных бингхэмовских пластических жидкостях движение начинается только после того, как напряжение сдвига превышает предельное значение. В псевдопласти ческих жидкостях некоторое движение возникает даже при низких напряжениях сдвига. При одинаковой энергоемкости и одинаковой геометрии реакторы с псевдопластической жидкостью заметно отличаются от реакторов с ньютоновской средой по задержке газа, распределению пузырьков по размеру и времени перемешивания.